⭐基础知识
代码随想录 (programmercarl.com)
什么是动态规划
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。
所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心 ,贪心没有状态推导,而是从局部直接选最优的,
动态规划的解题步骤
动态规划五部曲
确定dp数组(dp table)以及下标的含义 确定递推公式 dp数组如何初始化 确定遍历顺序 举例推导dp数组
动态规划应该如何debug
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果 。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
这样才是一个完整的思考过程,而不是一旦代码出问题,就毫无头绪的东改改西改改,最后过不了,或者说是稀里糊涂的过了 。
👉day12
198. 打家劫舍 - 力扣(LeetCode)
和第 198 题的不同之处是,这道题中的房屋是首尾相连的,第一间房屋和最后一间房屋相邻,因此第一间房屋和最后一间房屋不能在同一晚上偷窃。
难度中等1148
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
打家劫舍 II(动态规划,结构化思路,清晰题解) - 打家劫舍 II - 力扣(LeetCode)
本题dp[i] 表示前i家人口能抢劫到的最大金额
递推公式: dp[i]=Math.max(dp[i]-1,dp[i-2]+nums[i]);
初始状态:
前 0间房子的最大偷窃价值为 00 ,即 dp[0] = 0 。
遍历顺序从左至右
以前三家为例 : (假设房屋总数大于3 )
本题重点
也就是说不能同时抢劫第一间屋子以及最后一间屋子
如何才能保证第一间房屋和最后一间房屋不同时偷窃呢?
如果偷窃了第一间房屋,则不能偷窃最后一间房屋,因此偷窃房屋的范围是第一间房屋到最后第二间房屋;
如果偷窃了最后一间房屋,则不能偷窃第一间房屋,因此偷窃房屋的范围是第二间房屋到最后一间房屋。
假设数组 nums 的长度为 n。如果不偷窃最后一间房屋,则偷窃房屋的下标范围是 [0, n-2];
如果不偷窃第一间房屋,则偷窃房屋的下标范围是 [1, n-1]。
在确定偷窃房屋的下标范围之后,即可用第 198 题的方法解决。对于两段下标范围分别计算可以偷窃到的最高总金额,其中的最大值即为在 nn 间房屋中可以偷窃到的最高总金额。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { public int rob (int [] nums) { if (nums.length == 0 ||nums.length == 1 ) return nums.length==0 ?0 :nums[0 ]; return Math.max( DP(Arrays.copyOfRange(nums,0 ,nums.length-1 )), DP(Arrays.copyOfRange(nums,1 ,nums.length)) ); } public int DP (int []nums) { int n=nums.length; int []dp=new int [n+1 ]; dp[0 ]=0 ; dp[1 ]=nums[0 ]; for (int i = 2 ; i < dp.length; i++) { dp[i]=Math.max(dp[i-1 ],dp[i-2 ]+nums[i-1 ]); } return dp[n]; } }
难度中等1974
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
DP不会, 暴力一下
先确定能走到的, 通过num[i-1] 确定从当前的下标能到达后面的下标,
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public boolean canJump (int [] nums) { int n=nums.length; boolean []dp=new boolean [n+1 ]; dp[0 ]=true ; dp[1 ]=nums[0 ]>=0 ; for (int i = 1 ; i < dp.length-1 ; i++) { if (dp[i]){ for (int j = i; j <= i+nums[i-1 ]; j++) { if (j==dp.length) break ; dp[j]=true ; } } } return dp[n]; } }
贪心
初始化最远位置为 0,然后遍历数组,
如果当前位置能到达,并且当前位置+跳数>最远位置,就更新最远位置 。
最后返回res能否到达下标为n-1的位置
时间复杂度 O(n)
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public boolean canJump (int [] nums) { int n=nums.length; int res=0 ; for (int i = 0 ; i < nums.length; i++) { if (res>=i&&i+nums[i]>res){ res=i+nums[i]; } } return res>=n-1 ; } }
DP
从数组后往前看,如果某个位置能够到达最后,则可以把终点移到这个位置 b
1 2 3 4 5 6 7 8 9 10 class Solution { public boolean canJump (int [] nums) { int r = nums.length - 1 ; for (int i = nums.length - 2 ; i >= 0 ; i--) { if (nums[i] >= r - i) r = i; } return r == 0 ; } }
👉day 13
难度中等1773
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
假设你总是可以到达数组的最后一个位置。
【跳跃游戏 II】别想那么多,就挨着跳吧 II - 跳跃游戏 II - 力扣(LeetCode)
思路
如果某一个作为 起跳点 的格子可以跳跃的距离是 3,那么表示后面 3 个格子都可以作为 起跳点。
可以对每一个能作为 起跳点 的格子都尝试跳一次,把 能跳到最远的距离 不断更新。
如果从这个 起跳点 起跳叫做第 1 次 跳跃,那么从后面 3 个格子起跳 都 可以叫做第 2 次 跳跃。
所以,当一次 跳跃 结束时,从下一个格子开始,到现在 能跳到最远的距离,都 是下一次 跳跃 的 起跳点。
对每一次 跳跃 用 for 循环来模拟。
跳完一次之后,更新下一次 起跳点 的范围。
在新的范围内跳,更新 能跳到最远的距离。
代码如下 :
使用end来记录上一次跳跃到达的位置 , 如果i遍历到了end, 说明已经走到了 上一次到达的位置,
这时候让end赋值为从上一次到达的位置与当前的i位置之间能到达的最远的距离 maxDis, 也就达到了每一次都跳最远的距离的目的
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Solution { public int jump (int [] nums) { if (nums.length==1 ) return 0 ; int res=0 ,maxDis=0 ,end=0 ; for (int i = 0 ; i < nums.length-1 ; i++) { maxDis=Math.max(maxDis,i+nums[i]); if (i==end){ res++; end=maxDis; } } return res; } }
难度中等1529
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
DP
定义dp数组dp[][] , dp[i][j]代表的是走到(i,j)位置的路径总数
每一个格子的路径总数都等于它左边格子的路径+ 上边格子的路径
dp[i][j]=dp[i-1][j]+dp[i][j-1];
可以明白的是, 第一行以及第一列上的格子想要到达的路径只有一种
因此可以初始化第一行, 第一列的元素都为1 随后遍历非第一行第一列的格子, 依次计算出所有格子的路径
最后返回dp[m-1][n-1]
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution { public int uniquePaths (int m, int n) { int [][] dp=new int [m][n]; for (int i = 0 ; i < m; i++) dp[i][0 ]=1 ; for (int i = 0 ; i < n; i++) dp[0 ][i]=1 ; for (int i = 1 ; i < m; i++) { for (int j = 1 ; j < n; j++) { dp[i][j]=dp[i-1 ][j]+dp[i][j-1 ]; } } return dp[m-1 ][n-1 ]; } }
👉day 14
难度中等5642
给你一个字符串 s,找到 s 中最长的回文子串。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution { public String longestPalindrome (String s) { char []chars=s.toCharArray(); int res=0 ; int len = chars.length; for (int i=0 ;i<len;i++){ for (int x=0 ,y=len-i;y<=len;x++,y++){ if (isHw(s.substring(x,y).toCharArray())){ return s.substring(x,y); } } } return null ; } public boolean isHw (char []chars) { int len=chars.length; for (int i=0 ;i<len/2 ;i++){ if (chars[i]!=chars[len-i-1 ]) return false ; } return true ; } }
可以先看一看另一道相似的题
难度中等960
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串
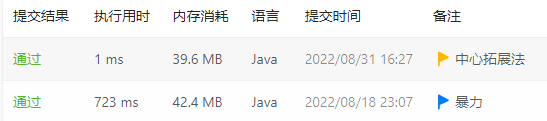
中心扩散法 ,调用count函数是计算以i或(i,i+1)为中心的回文串个数
可以看出效率相差巨大
思路
比如对一个字符串 ababa ,选择最中间的 a 作为中心点,往两边扩散,第一次扩散发现 left 指向的是 b,right 指向的也是 b,
所以是回文串,继续扩散,同理 ababa 也是回文串。
这个是确定了一个中心点后的寻找的路径,然后我们只要寻找到所有的中心点,问题就解决了。
本题代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution { int res=0 ; char []chars; public int countSubstrings (String s) { chars=s.toCharArray(); for (int i=0 ;i<chars.length;i++){ count(i,i); count(i,i+1 ); } return res; } public void count (int start, int end) { while (start >= 0 && end < chars.length && chars[start] == chars[end]){ res++; start--; end++; } } }
那么将这一题的代码稍作修改, 即可得到本题的代码
中心扩散法
遍历字符串, 每次都寻找回文子串,
维护left, right
分别为最长的子串的左下标与右下标
最后返回s.substring(left,right+1)即可
由于中心拓展的时候利用的是char数组 , 而String.substring(begin,end) 的区间是左闭右开, 因此需要right+1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { char []chars; int left=0x3f3f3f3f ; int right=-0x3f3f3f3f ; public String longestPalindrome (String s) { chars=s.toCharArray(); for (int i=0 ;i<chars.length;i++){ count(i,i); count(i,i+1 ); } return s.substring(left,right+1 ); } public void count (int start, int end) { while (start >= 0 && end < chars.length && chars[start] == chars[end]){ if (end-start>right-left){ left=start; right=end; } start--; end++; } } }
DP做法
中心扩散的方法,其实做了很多重复计算。动态规划就是为了减少重复计算的问题。动态规划听起来很高大上。其实说白了就是空间换时间,将计算结果暂存起来,避免重复计算。
思路
dp数组: 使用dp[l][r] 来记录L~R 的子串是否是回文
状态转移: 如果dp[l][r] 为true, 那么需要判断 chars[l] chars[r]是否相同,
相同: dp[l-1][r-1]为true ,继续判断
不同: 下一位
代码如下 :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution { public String longestPalindrome (String s) { int strLen = s.length(); int maxStart = 0 ; int maxEnd = 0 ; int maxLen = 1 ; boolean [][] dp = new boolean [strLen][strLen]; for (int r = 1 ; r < strLen; r++) { for (int l = 0 ; l < r; l++) { if (s.charAt(l) == s.charAt(r) && (r - l <= 2 || dp[l + 1 ][r - 1 ])) { dp[l][r] = true ; if (r - l + 1 > maxLen) { maxLen = r - l + 1 ; maxStart = l; maxEnd = r; } } } } return s.substring(maxStart, maxEnd + 1 ); } }
难度中等484
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
动态规划步骤
dp数组定义 : dp[i]表示以i为结尾, 数组为等差子数组的个数
状态转移 : 当前仅当当前元素与之前的两个元素构成等差数列的时候, dp[i] 才需要进行操作, 否则为0
当当前元素与前两个元素构成等差数列时, 由于dp[i]只与dp[i-1]有关, 可以得出状态转移为dp[i]=dp[i-1]+1
dp数组初始化 : 由于等差数列要求至少三个元素, 因此dp[i]均初始化为0
遍历方向以及范围: 从左向右顺序遍历 , 范围就是dp数组的所有数字
返回值: 题目要求计算所有的等差子数组的个数, 因此在遍历的过程中维护res , 累加dp[i] ,最后返回即可
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public int numberOfArithmeticSlices (int [] nums) { int res=0 ; if (nums.length<=2 ) return res; int []dp=new int [nums.length+1 ]; dp[0 ]=0 ; for (int i = 3 ; i < dp.length; i++) { if (nums[i-1 ]-nums[i-2 ]==nums[i-2 ]-nums[i-3 ]){ dp[i]=dp[i-1 ]+1 ; } res+=dp[i]; } return res; } }
为什么状态转移不是dp[i]=dp[i-1]+dp[i-2]+1 ?
因为判断的条件是 if(nums[i-1]-nums[i-2]==nums[i-2]-nums[i-3]) , 这个只能说明当前的元素与之前的两个元素是等差数列,
不能说明当前的元素与从前数第三个元素构成等差数列, 因此不能将dp[i-2]统计在内
👉day 15
难度中等1780
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
思路
对于输入的字符串s,如果我能够从单词列表wordDict中找到一个单词匹配s的前缀s[0..k],
那么只要我能拼出s[k+1..],就一定能拼出整个s。
这就相当于我们把规模较大的原问题wordBreak(s[0..])分解成了规模较小的子问题wordBreak(s[k+1..]),
然后通过子问题的解反推出原问题的解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution { HashSet<String> wordDict; int [] memo; public boolean wordBreak (String s, List<String> wordDict) { this .wordDict = new HashSet <>(wordDict); this .memo = new int [s.length()]; Arrays.fill(memo, -1 ); return dp(s, 0 ); } boolean dp (String s, int i) { if (i == s.length()) { return true ; } if (memo[i] != -1 ) { return memo[i] == 0 ? false : true ; } for (int len = 1 ; i + len <= s.length(); len++) { String prefix = s.substring(i, i + len); if (wordDict.contains(prefix)) { boolean subProblem = dp(s, i + len); if (subProblem) { memo[i] = 1 ; return true ; } } } memo[i] = 0 ; return false ; } }
难度困难630
给定一个字符串 s 和一个字符串字典 wordDict ,在字符串 s 中增加空格来构建一个句子,使得句子中所有的单词都在词典中。以任意顺序 返回所有这些可能的句子。
**注意:**词典中的同一个单词可能在分段中被重复使用多次。
回溯算法:单词拆分「超级无敌详细分析 🔥🔥🔥」 - 单词拆分 - 力扣(LeetCode)
回溯
每次写「回溯」题目时,就要思考三个问题:
路径:已经做出的选择
选择列表:当前可以做的选择
结束条件:到达决策树底层,无法再做选择的条件
我们现在结合样例
s = "catsanddog", wordDict = ["cat","cats","and","sand","dog"]
来梳理一下上面的三个问题!!
首先,我们的「结束条件」是什么?显然是当我们把 s 全部遍历完之后就可以结束
其次,我们的「选择列表」是什么?显然是 wordDict 中的单词集合
最后,我们的「路径」是什么?显然是我们每一步从 wordDict 中选择的单词集合
回溯树
可以很明显的看出需要剪枝的是在 wordDict 中找不到对应单词的分支
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution { Set<String> stringSet=new HashSet <>(); List<String> res=new ArrayList <>(); public List<String> wordBreak (String s, List<String> wordDict) { for (String str : wordDict) stringSet.add(str); backTrack(s,new LinkedList <>(),0 ); return res; } public void backTrack (String s, LinkedList<String> track,int start) { if (start==s.length()){ res.add(String.join(" " ,track)); return ; } for (int i = start; i < s.length(); i++) { String word=s.substring(start,i+1 ); if (!stringSet.contains(word)) continue ; track.add(word); backTrack(s,track,i+1 ); track.removeLast(); } } }
string.Join()方法
经常需要将一个数组或者List的各项通过分隔符连接成字符串。一般的实现逻辑是通过成员+分隔符连接,然后在结果截掉最后一个分隔符。突然,发现String.Join方法实现的正是这一功能。一个简单的例子输出a,b,c
1 2 3 4 5 6 7 8 9 10 11 12 13 class Program { static void Main (string[] args) { List<string> list=new List <string>(); list.Add ("a" ); list.Add ("b" ); list.Add ("c" ); Console.WriteLine (string.Join ("," ,list)); Console.ReadKey (); } }
结果: a b c
思路
难度中等1239
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
1 2 3 4 'A' -> "1" 'B' -> "2" ... 'Z' -> "26"
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,"11106" 可以映射为:
"AAJF" ,将消息分组为 (1 1 10 6)"KJF" ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 "06" 不能映射为 "F" ,这是由于 "6" 和 "06" 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
暴力
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 class Solution { public int numDecodings (String s) { if (s.length()==0 ) return 0 ; return process(s.toCharArray(),0 ); } public int process (char []chars,int i) { if (i==chars.length) return 1 ; if (chars[i]==0x30 ) return 0 ; if (chars[i]==0x31 ){ int res=process(chars,i+1 ); if (i+1 <chars.length){ res+=process(chars,i+2 ); } return res; }else if (chars[i]==0x32 ){ int res=process(chars,i+1 ); if (i+1 <chars.length&&chars[i+1 ]<=0x36 ){ res+=process(chars,i+2 ); } return res; } return process(chars,i+1 ); } }
DP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution { public int numDecodings (String s) { if (s.length()==0 ) return 0 ; char []chars=s.toCharArray(); int pre=1 ,cur=1 ; for (int i=1 ;i<s.length();i++){ int tmp=cur; if (chars[i]==0x30 ){ if (chars[i-1 ]==0x31 ||chars[i-1 ]==0x32 ){ cur=pre; }else { return 0 ; } } else if (chars[i-1 ]==0x31 ||(chars[i-1 ]==0x32 &&chars[i]<=0x36 )){ cur+=pre; } pre=tmp; } return cur; } }
😈同类型题目
难度简单2550
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
本问题其实常规解法可以分成多个子问题,爬第n阶楼梯的方法数量,等于 2 部分之和
爬上 n-1n−1 阶楼梯的方法数量。因为再爬1阶就能到第n阶
爬上 n-2n−2 阶楼梯的方法数量,因为再爬2阶就能到第n阶
排上 n 层 需要 先爬上 n-1 or n-2 层
注意本题是需要爬n ,不是爬到 n
0 1 2 3 4
1 1 2 3 5
1 2 3 4 5 6 7 8 9 10 11 12 13 class Solution {public : int climbStairs (int n) { int *res=new int [46 ]; res[0 ]=0 ; res[1 ]=1 ; res[2 ]=2 ; for (int i=3 ;i<=45 ;i++){ res[i]=res[i-1 ]+res[i-2 ]; } return res[n]; } };
写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
N 较小, 直接循环计算即可
需要注意的是 (a+b)%mod < = > (a%mod+b%mod)%mod
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { static final int mod=1000000007 ; public int fib (int n) { if (n==0 ) return 0 ; if (n==1 ||n==2 ) return 1 ; long f1=0L ,f2=1L ,f3=1L ; for (int i=1 ;i<n;i++ ) { long temp = f3; f3=(f1%mod+f2%mod)%mod; f1=f2; f2=f3; } return (int )f3%mod; } }
与上一题类似
1、
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 COPYclass Solution { public int numWays(int n) { // 1 1 2 3 return fib(n); } static int mod=1000000007; public int fib(int n) { if(n==2) return 2; if(n==1||n==0) return 1; long f1=1L,f2=1L ,f3=2L; for(int i=1;i<n;i++ ) { long temp =f3; f3=(f1%mod+f2%mod)%mod; f1=f2; f2=f3; } return (int)f3%mod; } }
2、
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 COPYclass Solution { static int mod=1000000007 ; int []res=new int [101 ]; public int numWays (int n) { res[0 ]=1 ; res[1 ]=1 ; res[2 ]=2 ; for (int i=3 ;i<=100 ;i++) { res[i]=(res[i-1 ]%mod+res[i-2 ]%mod)%mod; if (i==n) break ; } return res[n]; } }
3、 将上一个的数组替换为了HashMap ,可以节省内存
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { Map<Integer,Integer> res=new HashMap <>(); static int mod=1000000007 ; public int numWays (int n) { res.put(0 ,1 ); res.put(1 ,1 ); res.put(2 ,2 ); for (int i=3 ;i<=n;i++) { res.put(i,(res.get(i-1 )%mod+res.get(i-2 )%mod)%mod); } return res.get(n); } }
难度中等2225
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
当进行到 i 时, 可以选择 抢i or 不抢 i
抢 i ,就不能抢i-1 , dp[i]=dp[i-2]+nums[i]
不抢,dp[i]=dp[i-1];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import java.math.BigInteger;class Solution { public int rob (int [] nums) { int n=nums.length; int []dp=new int [n+1 ]; dp[0 ]=0 ; dp[1 ]=nums[0 ]; for (int i=2 ;i<=n;i++){ dp[i]=Math.max(dp[i-1 ],dp[i-2 ]+nums[i-1 ]); } return dp[n]; } }
难度中等1415
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为 root 。
除了 root 之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。
给定二叉树的 root 。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 ``` ## [120. 三角形最小路径和](https: 难度中等1077 给定一个三角形 `triangle` ,找出自顶向下的最小路径和。 每一步只能移动到下一行中相邻的结点上。**相邻的结点** 在这里指的是 **下标** 与 **上一层结点下标** 相同或者等于 **上一层结点下标 + 1 ** 的两个结点。也就是说,如果正位于当前行的下标 `i` ,那么下一步可以移动到下一行的下标 `i` 或 `i + 1 ` 。 image-20220731223914479 > 说白了就是找到从定点到底边的连线的最小sum > > 规则: > > - 只能走相邻的点 - dp思路 ,**自底向上** , - 定义`f (i , j )` 为第 `(i, j )`点到底边的最小距离 - 状态转移方程: - `f(i,j)=Math.min(f( i+1 ,j) ,f(i+1 , j+1 ) +triangle[i][j]` > `f( i+1 ,j) ,f(i+1 , j+1 )` 是 下一行的左右邻居 ```java COPY 2 3 4 6 5 0 4 1 8 1
自顶向上, dp[i][j] 表示的是 这个位置的坐标与下一行的较小的那个邻居的和
由于三角形的最底层没有下一行,因此需要多 new [n+1]
dp[][]:
4 1 8 1
7 2 1
2 5
4
每一个元素 的和 都是 最小值的理想情况,随着 层数的减小,元素个数不断减小 ,dp[0][0]只有两个可以选择的值, 此时dp[0][0]也就是最小值
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int minimumTotal (List<List<Integer>> triangle) { int n = triangle.size(); int [][]dp =new int [n+1 ][n+1 ]; for (int i=n-1 ;i>=0 ;i--){ for (int j = 0 ; j <=i ; j++) { dp[i][j]=Math.min(dp[i+1 ][j],dp[i+1 ][j+1 ]) + triangle.get(i).get(j); } } return dp[0 ][0 ]; } }
一维数组优化版本
由于许多层的数据只会使用一次,因此直接让后面的数据覆盖没用的数据, 节省空间
如果改为一维数组, 其实思路就是将 原来的二维数组的上面的行 直接在 下一行的位置赋值, 而且由于位置右移,
1 2 3 4 5 6 7 8 9 10 11 12 class Solution { public int minimumTotal (List<List<Integer>> triangle) { int n = triangle.size(); int []dp =new int [n+1 ]; for (int i=n-1 ;i>=0 ;i--){ for (int j = 0 ; j <=i ; j++) { dp[j]=Math.min(dp[j],dp[j+1 ]) + triangle.get(i).get(j); } } return dp[0 ]; } }
难度中等1476
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
DP 首先初始化长度为 n+1 的数组 dp,每个位置都为 0dp[i]=i,
比如 i=4,最坏结果为 4=1+1+1+1 即为 4 个数字
动态转移方程为:dp[i] = MIN(dp[i], dp[i - j * j] + 1),
i 表示当前数字,j*j 表示平方数时间复杂度:O(n∗sqrt(n)),sqrt 为平方根
代码
44ms
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 class Solution { public int numSquares (int n) { int [] dp = new int [n + 1 ]; for (int i = 1 ; i <= n; i++) { dp[i] = i; for (int j = 1 ; i - j * j >= 0 ; j++) { dp[i] = Math.min(dp[i], dp[i - j * j] + 1 ); } } return dp[n]; } }
数学解法
首先需要知道一个定理:
四平方和定理 : 任何一个正整数都可以表示成不超过四个整数的平方之和。 推论:满足四数平方和定理的数n(四个整数的情况),必定满足 n=4^a(8b+7)
通过这个定理, 相当于知道了
任何正整数都可以拆分成不超过4个数的平方和
如果一个数最少可以拆成4个数的平方和,则这个数还满足 n = (4^a)*(8b+7)
因此可以先看这个数是否满足上述公式,如果不满足,答案就是1,2,3了
如果这个数本来就是某个数的平方,那么答案就是1,否则答案就只剩2,3了
如果答案是2,即n=a2+b 2,那么我们可以枚举a,来验证,如果验证通过则答案是2
只能是3
代码如下
1ms
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public int numSquares (int n) { while (n % 4 == 0 ) n /= 4 ; if (n % 8 == 7 ) return 4 ; for (int i = 0 ; i * i <= n; ++i) { if (n - i * i == 0 ) return 1 ; } for (int i = 0 ; i * i < n; ++i) { for (int j = 0 ; j * j < n; ++j) { if (n - i * i - j * j == 0 ) return 2 ; } } return 3 ; } }
Last