leetcode题目(2)

typora编辑的md文件过长会导致卡顿, 因此继续分文件存笔记

🎈62. 不同路径: DP

难度中等1542

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

1. dp数组定义: dp[i][j]表示 走到下标为(i,j) 的种数,

2. 状态转移: 由于题目中规定机器人只能向下以及向右走, 那么对于当前的dp[i][j]

   dp[i][j]=dp[i-1][j]+dp[i][j-1]

   走到当前的坐标的路径种数就等于走到当前的坐标的左边以及上边的坐标的路径之和

3. dp数组初始化

   • 为了方便后续的计算,我们可以直接初始化 第一行以及第一列的元素为1 , 因为机器人只能往下往右走

   for (int i = 0; i < m; i++) dp[i][0]=1; for (int i = 0; i < n; i++) dp[0][i]=1;

4. 返回值: 返回dp[m-1][n-1] 表示走到终点的路径总数

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp=new int[m][n];// dp[i][j]表示走到i ,j 的路径的种数
        for (int i = 0; i < m; i++) dp[i][0]=1;
        for (int i = 0; i < n; i++) dp[0][i]=1;
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

🎈63. 不同路径 II :DP

难度中等876

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

本题与上一题的dp思路相同, 只需要做简单的处理即可

dp步骤可以直接参考上一题, 下面简单叙述需要注意的地方

1. 在初始化的时候, 如果遇到了障碍物, 那么当前的坐标以及后面的坐标都不可能达到 (机器人只能向下向右走), 因此需要改变初始化的方式

   在遇到障碍物的时候直接break即可

2. 状态转移的过程中,

   • 如果没有遇到障碍物 , 那么与上一题完全相同
   • 如果遇到了障碍物, 则直接跳过当前的坐标, 或者写成dp[i][j]=0

代码如下

class Solution {
    public int uniquePathsWithObstacles(int[][] board) { // 存在某个位置是1 ,表示障碍物
        int m=board.length,n=board[0].length;
        int[][] dp=new int[m][n];// dp[i][j]表示走到i ,j 的路径的种数
        for (int i = 0; i < m; i++){
            if(board[i][0]==1) break;
            dp[i][0]=1;
        }
        for (int j = 0; j < n; j++) {
            if(board[0][j]==1) break;
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if(board[i][j]==1) continue;
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

🗝️等差数列划分 : DP

难度中等486

如果一个数列 至少有三个元素 ，并且任意两个相邻元素之差相同，则称该数列为等差数列。

• 例如，[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。

给你一个整数数组 nums ，返回数组 nums 中所有为等差数组的 子数组 个数。

子数组 是数组中的一个连续序列。

第一次写这个题的时候还不是很理解dp[i]的含义, 第二次就很自然的理解了

DP步骤:

1. dp数组定义 : dp[i] 表示0~i 以dp[i]中等差数列的个数
2. 状态转移 :
   • 如果当前的数组与前两个数组构成了等差数列, 那么 dp[i]=dp[i-1]+1;
   • 否则的话就是dp[i]=0
3. 初始化 : 所有位置都初始化为 0
4. 返回值 : 在DP结束后, 求和返回即可

class Solution {
    public int numberOfArithmeticSlices(int[] nums) {
        int res=0; 
        if(nums.length<=2) return res;
        int[]dp=new int[nums.length];// dp[i] 表示0~i 以dp[i]中等差数列的个数
        for (int i = 2; i < dp.length; i++) {
            if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2])
                dp[i]=dp[i-1]+1;
        }
        for (int i = 0; i < dp.length; i++) {
                System.out.println(dp[i]);
            res+=dp[i];
        }
        return res;
    }
}

🗝️91. 解码方法

难度中等1251

一条包含字母 A-Z 的消息通过以下映射进行了 编码 ：

'A' -> "1"
'B' -> "2"
...
'Z' -> "26"

要 解码 已编码的消息，所有数字必须基于上述映射的方法，反向映射回字母（可能有多种方法）。例如，"11106" 可以映射为：

• "AAJF" ，将消息分组为 (1 1 10 6)
• "KJF" ，将消息分组为 (11 10 6)

注意，消息不能分组为 (1 11 06) ，因为 "06" 不能映射为 "F" ，这是由于 "6" 和 "06" 在映射中并不等价。

给你一个只含数字的 非空 字符串 s ，请计算并返回 解码 方法的 总数 。

题目数据保证答案肯定是一个 32 位 的整数。

本题的思路类似于斐波那契数列,

Dp思路

1. dp数组定义: dp[i] 表示0~i-1 范围内的解码方法数
2. 状态转移:
3. dp数组初始化 : 根据dp数组的定义, 初始化dp[0]=1
4. 返回值: 返回dp[n] 的解码方法数

class Solution {
    public int numDecodings(String s) {
        if(s.charAt(0)==0x30) return 0;
        int n=s.length();
        char[]chars=s.toCharArray();
        int[]dp=new int[n+1];// dp[i] 表示0~i 下标的编码的总数
        dp[0]=1;
        for(int i=1;i<=n;i++){
            if(chars[i-1]!=0x30){
                dp[i]+=dp[i-1];
            }
            if(i>1&&chars[i-2]!=0x30&&((chars[i-2]-0x30)*10+chars[i-1]-0x30<=26))
                dp[i]+=dp[i-2];
        }
        return dp[n];
    }
}

42. 接雨水

难度困难3795

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

暴力解法

• 求出每一个位置可以存储的水量, 求和

从当前位置分别从两边开始计算, 获取两边的最高的柱子,

最后通过两边最高的柱子比当前的柱子多出的高度来计算蓄水量

class Solution {
    public int trap(int[] height) {
        int res=0;
        for (int i = 1; i < height.length-1; i++) {// 暴力求每个位置可以装的最多的雨水
            int l_max=height[i],r_max=height[i];
            for (int l = 0; l < i; l++) {
                l_max=Math.max(height[l],l_max);
            }
            for (int r = i+1; r < height.length; r++) {
                r_max=Math.max(height[r],r_max);
            }
            res+=Math.min(l_max-height[i],r_max-height[i]);
        }
        return res<0?0:res;
    }
}

暴力解法优化: 备忘录

使用l_max[] ,r_max[] 存储前i天以及后i天 最大的柱子高度 , 需要使用的时候直接调用即可 , 省去了冗余的计算

class Solution {
    public int trap(int[] height) {
        int n=height.length;
        int res=0;
        int[]l_max=new int[n];
        int[]r_max=new int[n];
        l_max[0]=height[0]; // l_max[i] 表示 前i天最高的柱子高度
        r_max[n-1]=height[n-1];//l_max[i] 表示后i天最高的柱子高度
        for (int i = 1; i < n; i++)
            l_max[i]=Math.max(l_max[i-1],height[i]);
        for (int i = n-2; i >=0; i--)
            r_max[i]=Math.max(r_max[i+1],height[i]);

        for (int i = 1; i < n-1; i++) {// 求每个位置可以装的最多的雨水
            res += Math.min(l_max[i], r_max[i]) - height[i];
        }
        return res;
    }
}

🎈11. 盛最多水的容器

难度中等3769

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

**说明：**你不能倾斜容器。

思路:

面积 :math.min(height[i],height[j])*( j-i)

双指针:

1. 定义左右两个指针, 分别指向数组左右两侧
2. 每次向里面收缩 i ,j 中的较短的那个板, 维护res
   • i, j 相遇时结束
3. 最会返回res

• 注意(j-i)*height[i++] 以及(j-i)*height[j--] 的相乘的顺序, 需要吧 j-i 放到前面, 否则会少乘

每次收缩短板的原因:

• 若向内 移动短板 ，水槽的短板 min(h[i],h[j])可能变大，因此下个水槽的面积 可能增大 。
• 若向内 移动长板 ，水槽的短板min(h[i], h[j])不变或变小，因此下个水槽的面积一定变小
  • 注意 : 水槽的面积取决于短板以及底部的宽度 , 因此我们需要想办法让短板变得更大 , 所以说移动长板水槽的总面积一定会减小

class Solution {
    public int maxArea(int[] height) {
        int res=0;
        int i=0,j=height.length-1;
        while(i<j){
            res=height[i]<height[j]?Math.max(res,(j-i)*height[i++]):Math.max(res,(j-i)*height[j--]);
        }
        return res;
    }
}

670. 最大交换

难度中等350

给定一个非负整数，你至多可以交换一次数字中的任意两位。返回你能得到的最大值。

思路

将数字从大到小排列，与原数字比较，找出第一位置不一样的数。如8217排序后变为8721，两两对比，第二个数不同，表示7和2交换，得到结果8712

思路简单, 实现起来有点麻烦

• 注意数字重复的情况需要从后面选取

  从后往前能保证最大。大数换到前头，小数去了最后头

代码如下

class Solution {
 public int maximumSwap(int num) {
        String s=String.valueOf(num);// 85719  => 98751
        char[]chars=s.toCharArray();
        Arrays.sort(chars);
        reverse(chars);
        for (int i = 0; i < chars.length; i++) {
            if(chars[i]!=s.charAt(i)){
                for (int j = s.length()-1; j >i ; j--) {
                    if(s.charAt(j)==chars[i]){
                        s=swap(s,i,j);
                        return Integer.parseInt(s);
                    }
                }
            }
        }
        //将数字从大到小排列，与原数字比较，找出第一位置不一样的数。
        //如8217排序后变为8721，两两对比，第二个数不同，表示7和2交换，得到结果8712
        //注意数字重复的情况需要从后面选取
        return num;
    }
    void reverse(char[]chars){
        int len=chars.length;
        for (int i = 0; i < len/2; i++) {
            char tmp=chars[i];
            chars[i]=chars[len-i-1];
            chars[len-i-1]=tmp;
        }
    }
    String swap(String s,int i,int j){
        char[]chars=s.toCharArray();
        chars[i]=s.charAt(j);
        chars[j]=s.charAt(i);
        return new String(chars);
    }
}

221. 最大正方形: DP

难度中等1266

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积

DP思路:

1. dp数组定义: dp[i][j] 表示当前的格子能以参与构成的正方形的最大面积

2. 状态转移 : 当我们需要判断某个格子是是否能参与构成正方形时, 这个格子本身必须是1 , 如果想要参与构成更大方的正方形, 那么这个格子的上方左方斜向上左方都需要是1 ,

   • 如果当前的格子是0 ,直接跳过

   • 如果是1, 那么方程为dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;

     取前面提到的三个格子的最小值,

   

   图 1：受限于左上的 0
   图 2：受限于上边的 0
   图 3：受限于左边的 0
   数字表示：以此为正方形右下角的最大边长
   黄色表示：格子 ? 作为右下角的正方形区域
   就像 木桶的短板理论 那样——附近的最小边长，才与 ? 的最长边长有关。

3. dp数组初始化: 初始化第一行以及第一列的元素, 如果元素是1 那么就初始化1, 反之为0

   注意需要在初始化的过程中就开始维护res, 因为测试样例可能只有一行或者一列

4. 返回值: 在DP的过程中维护res, 统计最大的正方形的边长, 最后返回 res*res

class Solution {
public int maximalSquare(char[][] matrix) {
        /*当 matrix[i][j] 为 1，且它的左边、上边、左上边都存在正方形时，
        matrix[i][j] 才能够作为一个更大的正方形的右下角：* */
        int m=matrix.length,n=matrix[0].length;
        int[][]dp=new int[m][n];// dp[i][j]表示 i,j位置的最大的正方形的面积
        dp[0][0]=matrix[0][0]-0x30;
        int res=dp[0][0];
        for (int i = 1; i < m; i++) {
            dp[i][0]=matrix[i][0]-0x30;
            res=Math.max(res,dp[i][0]);
        }
        for (int j = 1; j < n; j++) {
            dp[0][j]=matrix[0][j]-0x30;
            res=Math.max(res,dp[0][j]);
        }
        for (int i = 1; i < matrix.length; i++) {
            for (int j = 1; j < matrix[i].length; j++) {
                if(matrix[i][j]!=0x30){
                    dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
                }
                res=Math.max(res,dp[i][j]);
            }
        }
        return res*res;
    }
}

29. 两数相除

难度中等978

给定两个整数，被除数 dividend 和除数 divisor。将两数相除，要求不使用乘法、除法和 mod 运算符。

返回被除数 dividend 除以除数 divisor 得到的商。

整数除法的结果应当截去（truncate）其小数部分，例如：truncate(8.345) = 8 以及 truncate(-2.7335) = -2

递归

• 每次扩大被除数的二倍, 同时商*2 , 递归求解

核心代码

int div(long a,long b){// a 为 被除数, b为除数
    if(a<b) return 0;
    long operateB=b;
    int count=1;
    while(a-operateB*2>=0){
        operateB*=2;
        count*=2;
    }
    return count+div(a-operateB,b);
}

下面以 64, 5 为例, 详细叙述过程

首先是 a=64, b=5

• operateB :5=>10=>20=>40 , operateB=40 的时候不在满足(a-operateB*2>=0) , 此时进入下一层递归

  对应的`count: 1=>2=>4=>8`
  

• 第二层递归:

  a=24, b=5

  5=>10=>20

  1=>2=>4

• 第三层递归

  a=4 , b=5 => return 0

那么总的来看, 我们将64分为了 40+20+4, 对应的商分别为8+4

边界问题🙄

思路不难, 需要注意一些边界问题

1. 注意正负问题, 由于我们计算的实质是加减法计算, 因此需要都变成正数再去计算
   • 注意-Integer.MIN_VALUE != Integer.MAXVALUE , 所以计算的时候需要把除数和被除数使用long存储
2. 注意除数为1 or -1, 特殊处理即可

完整代码如下

class Solution {
    public int divide(int dividend, int divisor) {// 除数: divisor  被除数: dividend  本题所求: dividend/divisor : a/b
        if(dividend == 0) return 0;
        if(1==divisor) return dividend;
        if(divisor==-1){
            if(dividend>Integer.MIN_VALUE) return -dividend;
            return Integer.MAX_VALUE; // 越界 ,返回Integer最大值
        }
        boolean isSameOperate=true;// 是否同号
        long a=dividend,b=divisor;
        if((a>0&&b<0) || (a<0&&b>0)){
            isSameOperate=false;
        }
        a = a>0?a:-a;
        b = b>0?b:-b;
        long res=div(a,b);
        if(isSameOperate){// 同号
            return res>Integer.MAX_VALUE?Integer.MAX_VALUE:(int)res;
        }
        return (int) -res;
    }
    int div(long a,long b){
        if(a<b) return 0;
        long operateB=b;
        int count=1;
        while(a-operateB*2>=0){
            operateB*=2;
            count*=2;
        }
        return count+div(a-operateB,b);
    }
}

---

5. 最长回文子串

难度中等5704

给你一个字符串 s，找到 s 中最长的回文子串。

中心扩散法

遍历每个字符, 从每个字符为中心, 计算回文子串的最大长度void count()

• left, right 负责统计最长的回文子串的左右下标,

  注意计算的时候用的是字符数组, 最后使用substring() 返回的时候需要 right+1 , 因为substring 方法的区间是左闭右开

具体细节参考代码实现:

class Solution {
    char[]chars;
    int left=0x3f3f3f3f; 
    int right=-0x3f3f3f3f;
    public String longestPalindrome(String s) {
        chars=s.toCharArray();
        for(int i=0;i<chars.length;i++){
            count(i,i); // 子串长度为奇数
            count(i,i+1); //子串长度为偶数
        } //  12321
        return s.substring(left,right+1); // substring  左闭右开
    }

    public void count(int start, int end){
        while(start >= 0 && end < chars.length && chars[start] == chars[end]){ // 中心拓展法 , 从中间开始 ,向两边扩张
            if(end-start>right-left){
                left=start;
                right=end;
            }
            start--;
            end++;
        }
    }
}

DP做法

DP思路

1. dp数组含义: dp[l][r]表示 l~r 区间的子串是否回文, true表示回文, false 为其他情况 boolean[][]dp

   另一种做法是dp[i][j] 统计当前的回文子串的长度

   dp[i][j]=dp[i+1][j-1]+2

   • 其他情况:
     • s[i, j]本身不是一个回文串；
     • i>j，此时 s[i, j]本身不合法。

2. 状态转移 :

   • chars[i]==char[j]时 , dp[l][r]= dp[l+1][r-1] && chars[i]==chars[j]
   • 不相等时, dp[i][j]=false

3. dp数组初始化 : 初始化 dp[i][i]=true , dp[i][i+1]=chars[i]==chars[i+1]

4. 返回值 : 在DP的过程中维护maxLen以及 begin, 最终返回s.substring(begin,begin+maxLen);

代码如下

public class Solution {
    public String longestPalindrome(String s) {
        int n = s.length();
        if(n<2) return s;
        int begin = 0;  //最长回文串的起点
        int maxLen = 1;  //最长回文串的长度
        char[]chars=s.toCharArray();
        boolean[][] dp = new boolean[n][n];// dp[i][j] 表示 i~j 是否为回文子串
        for (int i = 0; i < chars.length; i++) {// dp数组初始化 :
            dp[i][i]=true;
        }//abbba
        for (int L = 2; L <=n; L++) {// L 表示字串的长度
            for (int i = 0; i < n; i++) {
                int l=i;
                int r=L+i-1;//右下标
                if(r>=n){
                    break;
                }
                if(chars[l]==chars[r]){
                    if(r-l<3){
                        dp[l][r]=true;
                    }else{
                        dp[l][r]=dp[l+1][r-1];
                    }
                }
                if(dp[l][r]&&maxLen<r+1-l){
                    maxLen=r+1-l;
                    begin=l;
                }
            }
        }
        return s.substring(begin,begin+maxLen);
    }
}

516. 最长回文子序列 : DP

难度中等886

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

DP思路

1. dp数组含义: dp[i][j]表示 i~j 区间的最长回文子序列的长度

   • 其他情况:
     • s[i, j]本身不是一个回文串；
     • i>j，此时 s[i, j]本身不合法。

2. 状态转移 : chars[i]==char[j]时, 当前的回文子序列长度+2, dp[i][j]=dp[i+1][j-1]+2

   不相等的时候, dp[i][j]=Math.max(dp[i][j-1],dp[i+1][j])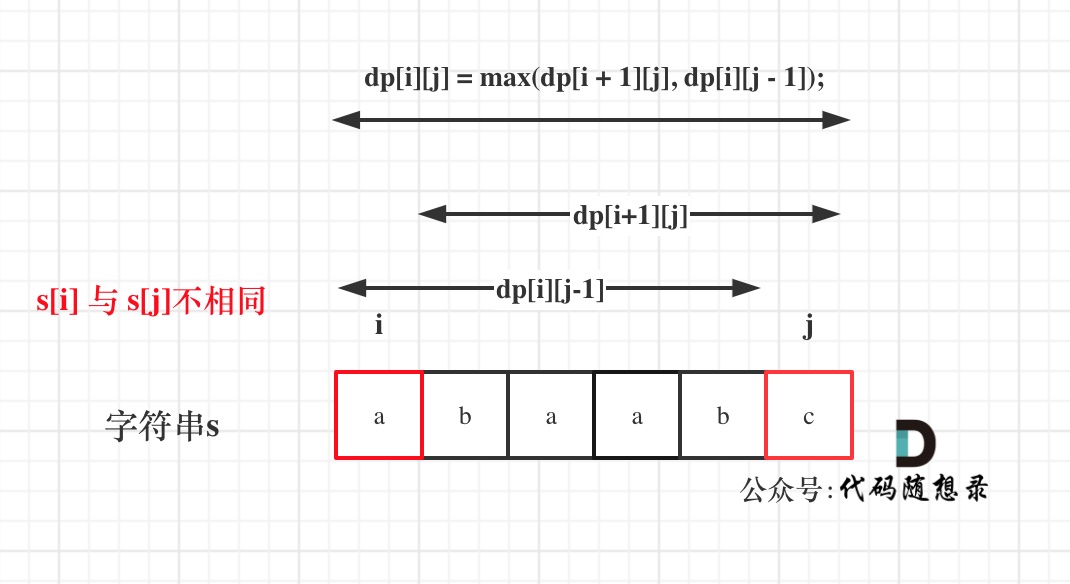

   

   由于这里我们计算dp[i][j]的时候可能会用到dp[i+1][j], 因此我们需要倒序遍历 , 使得dp[i+1][j] 是计算之后的, 否则会有错误

3. dp数组初始化 : 初始化 dp[i][i]=1

4. 返回值 : 在DP的过程中维护res统计最长的回文子序列的长度, 最后返回即可

代码如下

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n=s.length();
        if(s.length()<2) return 1;
        int res=1; //返回最长的回文子序列
        char[]chars=s.toCharArray();
        int[][]dp=new int[n][n]; //dp[i][j] 表示i~j 的最长的回文子序列的长度
        for (int i = 0; i < n; i++) {
            dp[i][i]=1;
        }
        for (int i = n-1; i >=0; i--) {
            for (int j = i+1; j < n; j++) {
                if(chars[i]==chars[j]){
                    dp[i][j]=dp[i+1][j-1]+2;
                }else{
                    dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
                }
                res=Math.max(res,dp[i][j]);
            }
        }
        return res;
    }
}

300. 最长递增子序列 : DP

难度中等2787

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

dp思路

1. dp数组含义, : dp[i] 代表以nums[i] 结尾时, 数组的最长递增子序列

2. 状态转移: 我们从当前的数组往前遍历 , 当遇到了比当前的num[i] 小的数时, 那么dp[i]=Math.max(dp[i],dp[j]+1)

   对于每个nums[i] 都遍历他之前的元素, (倒序遍历), 如果遍历到的元素比当前的元素小, 那么就dp[i]=Math.max(dp[i].dp[j]+1);

3. dp数组初始化 : 由于每一个子序列至少含有一个元素, 因此dp数组的所有元素都应该初始化为 1

4. 遍历方向以及范围: 从左向右顺序遍历 , 范围就是dp数组的所有数字

5. 返回值 : 在遍历的过程中, 维护res , 每次都取最大值, 最后返回 , 记为最长递增子序列

第二层循环正倒序遍历都是可以的

class Solution {
    /*
    正序遍历与 倒序遍历没啥区别 
     */
    public int lengthOfLIS(int[] nums) {
        if(nums.length==1) return 1;
        int res=0;
        int[]dp=new int[nums.length]; //dp[i]表示 以nums[i]结尾的最长的递增的子序列的长度
        Arrays.fill(dp,1);
        dp[0]=1;
        /// 对于每个nums[i] 都遍历他之前的元素, (倒序遍历), 如果遍历到的元素比当前的元素小, 那么就dp[i]=Math.max(dp[i].dp[j]+1);
        for (int i = 0; i < nums.length; i++) {
//                for (int j = i-1; j >=0; j--) {
            for (int j = 0; j <i; j++) {
                if(nums[i]>nums[j]){
                    dp[i]=Math.max(dp[i],dp[j]+1);
                }
                res=Math.max(res,dp[i]);
            }
        }
        return res;
    }
}

376. 摆动序列

难度中等759

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列 。**第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

• 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
• 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

贪心

贪心思路 清晰而正确的题解 - 摆动序列 - 力扣（LeetCode）

新的数字与之前的数字只有三种关系, 大于, 小于, 等于, 对于等于的情况我们不予考虑

变量含义:

• up 表示当前的摆动序列最后的元素是上升的元素的长度 , 例如1,7,2,3
• down 表示当前的摆动序列最后的元素是下降的元素的长度 , 例如1,7,2,3,4

我们在遍历数组元素的过程中统计两种摆动序列的长度, 最终返回两者之中的最大值

代码如下

class Solution {
    public int wiggleMaxLength(int[] nums) {
        // 贪心做法
        if(nums.length<2) return nums.length;
        int up=1,down=1;
        for (int i = 1; i < nums.length; i++) {
            if(nums[i]>nums[i-1]){
                up=down+1;
            }else if(nums[i]<nums[i-1]){
                down=up+1;
            }
        }
        return Math.max(up,down);
    }
}

DP做法

• 一种dp 的思路是使用二维DP, 创建 类似于上面贪心的思路的 up down 数组

贴一个官方代码

class Solution {
    public int wiggleMaxLength(int[] nums) {
        int n = nums.length;
        if (n < 2) {
            return n;
        }
        int[] up = new int[n];
        int[] down = new int[n];
        up[0] = down[0] = 1;
        for (int i = 1; i < n; i++) {
            if (nums[i] > nums[i - 1]) {
                up[i] = Math.max(up[i - 1], down[i - 1] + 1);
                down[i] = down[i - 1];
            } else if (nums[i] < nums[i - 1]) {
                up[i] = up[i - 1];
                down[i] = Math.max(up[i - 1] + 1, down[i - 1]);
            } else {
                up[i] = up[i - 1];
                down[i] = down[i - 1];
            }
        }
        return Math.max(up[n - 1], down[n - 1]);
    }
}

其他写法

• 通过op数组记录每两个元素的差值, res代表最后的摆动序列的长度

  • res 初始化为2, 因为如果两个元素的差不为0 , 那么序列的长度至少为2

• 记录前一个差值的状态

  如果相邻的两个元素满足摆动序列的定义, 那么久res++

中间需要注意的问题

1. 前面有多个元素相等

   • 通过while循环去除前面的0 元素

   需要注意边界问题

class Solution {
    public int wiggleMaxLength(int[] nums) {
        //if(nums.length<2) return nums.length;  这两个特殊情况下面的start 也可以处理
        //if(nums.length==2) return nums[0]==nums[1]?1:2;
        int[]op=new int[nums.length-1];
        for (int i = 1; i < nums.length; i++) {
            op[i-1]=nums[i]-nums[i-1];
        }
        int start=0;// 统计 差不为0的相邻元素的 起始下标
        while(start<op.length&&op[start]==0){
            start++;
        }
        if(start>=op.length){// 注意边界问题 , 这里是对应的前面的元素全都相等的情况
            return 1;
        }
        boolean statusBigZero=op[start]>0;// 表示前面的差与0的关系
        int res=2;
        for (int i = start; i < op.length; i++) {
            if(statusBigZero&&op[i]<0){
                statusBigZero=false;
                res++;
            }else if(!statusBigZero&&op[i]>0){
                statusBigZero=true;
                res++;
            }
        }
        return res;
    }
}

---

🗝️1143. 最长公共子序列 :DP

难度中等1118

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

• 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

动态规划步骤:

1. dp数组定义: 本题是两个字符串, 那么优先采用 二维数组, dp[i][j] 表示的是 第一个字符串的[0:i] 与第二个字符串的[0:j的最长公共子序列
2. 状态转移:
   • 当s1[i]与s2[j] 相等时, 说明两个子串的最后一位相等, 此时最长公共子序列+1 dp[i][j]=dp[i-1][j-1]+1
   • 如果当前的两个字符不相同, 那么当前的dp数组的值根据之前的值得出, dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
3. 状态的初始化 : 初始化也就是看i=0或者,j=0的时候,dp[i][j]取多少,
   • 当 i = 0 时，dp[0][j]表示的是 text1 中取空字符串 跟 text2 的最长公共子序列，结果肯定为 0.
   • 当 j = 0 时，dp[i][0]表示的是 text2 中取空字符串 跟text1 的最长公共子序列，结果肯定为 0
4. 遍历方向与范围:
   • 遍历方向: 顺序遍历
   • 范围, 注意dp数组的大小是new int[s1.length+1][s2.length+1] , 由于 i=0, j=0已经初始化, 所以直接从 i=1 ,j=1开始遍历, 遍历应该在遍历完字符串的时候结束, 也就是 i<=s1.length ;j<s2.length
5. 最终返回结果: 结合dp数组的含义 ,最终返回 dp[s1.length][s2.length]

代码如下

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        char[]s1=text1.toCharArray();
        char[]s2=text2.toCharArray();
        int len=Math.max(s1.length,s2.length);
        int [][]dp=new int[s1.length+1][s2.length+1];
        dp[0][0]=0; // 空字符串 , 序列都为0 ,因此初始化为0   dp[i][j] 表示的是 s1 0~i-1 s2 0~-1j 的最长公共子序列
        for (int i = 1; i <= s1.length; i++) {
            for (int j = 1; j <= s2.length; j++) {
                if(s1[i]==s2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);
                }
            }
        }
        return dp[s1.length][s2.length];
    }
}// ac  abc 

🗝️72. 编辑距离 :DP

难度困难2598

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

• 插入一个字符
• 删除一个字符
• 替换一个字符

动态规划步骤:

1. dp数组定义: 本题是两个字符串, 那么优先采用 二维数组, dp[i][j]表示 word1以i-1结尾出现的word2以j-1结尾 达到相同 需要删除的次数

2. 状态转移:

   • 当w1[i]与w2[j] 相等时, 此时不需要删除任何字符 dp[i][j]=dp[i-1][j-1]

   • 如果当前的两个字符不相同, 那么当前的dp数组的值根据之前的值得出

     1. 删除w1[i-1] 对应的方程就是 dp[i][j]=dp[i-1][j]+1;
     2. 删除w2[j-1] 对应的方程就是 dp[i][j]=dp[i][j-1]+1;
     3. 替换元素, 直接把w1 或者 w2 的当前的元素替换, 使其与另一个元素相同, 此时不需要添加或者删除元素, 操作数就是dp[i][j]+1

     那么当然是选最小值删除, 因此递推公式为:

     dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]))+1;

   为什么这里都是删除元素, 没有添加元素呢?

   • word2删除一个元素, 就相当于word1添加一个元素

   举例

   • word1=“ad” ,word2=“a” ,
   • word1 删除’d’ 与 word2 增加’d’ , 最终的操作数是一样的

3. 状态的初始化 : 初始化也就是看 i=0或者,j=0的时候,dp[i][j]取多少,

   • 当 i = 0 时，dp[i][0] i个字符到空串需要删除i次
   • 当 j = 0 时，dp[0][j] j个字符到空串需要删除j次

4. 遍历方向与范围:

   • 遍历方向: 顺序遍历
   • 范围, 注意dp数组的大小是new int[w1.length+1][w2.length+1] ,
   • 由于 i=0, j=0已经初始化, 所以直接从 i=1 ,j=1开始遍历, 遍历应该在遍历完字符串的时候结束, 也就是 i<=w1.length ;j<=w2.length

5. 最终返回结果: 结合dp数组的含义 ,最终返回 dp[w1.length][w2.length]

代码如下

class Solution {
    public int minDistance(String word1, String word2) {
        int[][]dp=new int[word1.length()+1][word2.length()+1]; //// dp[i][j]表示  word1以i-1结尾出现的word2以j-1 结尾 达到相同 需要删除的次数
        char[]w1=word1.toCharArray();
        char[]w2=word2.toCharArray();
        // 变成空串只能删除
        for (int i = 0; i < dp.length; i++) { //初始化 一个字符到空串需要删除一次 ,
            dp[i][0]=i;
        }
        for (int j = 0; j < dp[0].length; j++) {//初始化 一个字符到空串需要删除一次
            dp[0][j]=j;
        }
        for (int i = 1; i < dp.length; i++) {//bagg  bag
            for (int j = 1; j < dp[i].length; j++) {
                if(w1[i-1]==w2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
                    // 分别对应添加/修改, 替换
                }
            }
        }
        return dp[w1.length][w2.length];
    }
}

392. 判断子序列

难度简单731

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

双指针

定义一个指针指向s的首个元素, 遍历t, 当s[i]==t[i] , 指针移动指向下一个元素,

最后返回指针是否能遍历完s

class Solution {
    public boolean isSubsequence(String s, String t) {
        int[][]dp=new int[s.length()+1][t.length()+1]; //// dp[i][j]表示  w1以i-1结尾出现的word2以j-1 结尾 达到相同 需要删除的次数
        char[]s1=s.toCharArray();
        char[]t1=t.toCharArray();
        int ptr=0;
        for (int j = 0; j < t1.length; j++) {
            if(ptr>=s1.length)
                return true;
            if(s1[ptr]==t1[j])
            {
                ptr++;
            }
        }
        return ptr>=s1.length?true:false;
    }
}

118. 杨辉三角

难度简单839

给定一个非负整数 *numRows，*生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

我们先添加上一行的第一个元素, 然后使当前的元素与上一行的右邻居一一对应, 最后在添加上一行的最后一个元素即可

class Solution {
    public List<List<Integer>> generate(int n) {
        var res=new ArrayList<List<Integer>>();
        if(n==0) return res;
        LinkedList<Integer> list=new LinkedList<>();
        list.add(1);
        res.add(list);
        for (int i = 1; i < n; i++) {
            LinkedList<Integer> tmp=new LinkedList<>();
            tmp.add(list.getFirst()); // 添加第一个元素
            for (int j = 1; j < list.size(); j++) {
                tmp.add(list.get(j-1)+list.get(j));//添加中间元素
            }
            tmp.add(list.getLast());//添加上一行的末尾元素
            list=new LinkedList<>(tmp); // 更新list为当前行
            res.add(tmp);//添加当前行
        }
        return res;
    }
}

119. 杨辉三角 II

难度简单428

给定一个非负索引 rowIndex，返回「杨辉三角」的第 rowIndex 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

与上一题思路相同, 返回指定行即可

注意[1] 是第零行👿

class Solution {
    public List<Integer> getRow(int n) {
        LinkedList<Integer> list=new LinkedList<>();
        list.add(1);
        if(n==0) return list;
        for (int i = 0; i < n; i++) {
            LinkedList<Integer> tmp=new LinkedList<>();
            tmp.add(list.getFirst()); // 添加第一个元素
            for (int j = 1; j < list.size(); j++) {
                tmp.add(list.get(j-1)+list.get(j));//添加中间元素
            }
            tmp.add(list.getLast());//添加上一行的末尾元素
            list=new LinkedList<>(tmp); // 更新list为当前行
        }
        return list;
    }
}