题目 🍐

4. 寻找两个正序数组的中位数

难度困难6151

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个==正序数组==的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2
示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

这个题目既然要求了

算法的时间复杂度应该为 O(log (m+n))

那么必然是用到了二分相关的思想

那么回顾一下中位数的定义，

如果某个有序数组长度是奇数，那么其中位数就是最中间那个，如果是偶数，那么就是最中间两个数字的平均值。

这里对于两个有序数组也是一样的，假设两个有序数组的长度分别为m和n，由于两个数组长度之和 m+n 的奇偶不确定，因此需要分情况来讨论，对于奇数的情况，直接找到最中间的数即可，偶数的话需要求最中间两个数的平均值。

为了简化代码，不分情况讨论，我们可以这样来计算，我们分别找第 (m+n+1) / 2 个，和 (m+n+2) / 2 个，然后求其平均值即可，这对于奇偶数均适用。

假如m+n 为奇数的话，那么其实 (m+n+1) / 2 和 (m+n+2) / 2 的值相等，相当于两个相同的数字相加再除以2，还是其本身。

我们可以这样来做 , 对于一次操作 , 我们每次从总的数组中排除一些必然不可能是中位数的数字

具体的做法

我们统计 两个数组的总长度 ,然后通过这个总长度来计算中位数的下标 , 我们记为k(k为中位数的下标),

那么一定会有这种的情况, 中位数位于某一个数组的 必然是 0< idx < k

那么我们可以 每次取到 两个数组的k/2 的位置的下标, 在这个位置 前面总共有k or k-1 (如果k是奇数)个元素

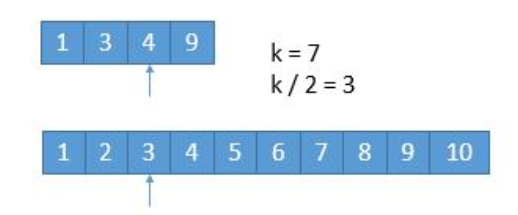
那么在这两个数组分开的部分中, 一定会有一个数组的 这一部分 不能可能存在中位数 (条件是 这个数组的当前部分的最右边的元素小于另一个数组的) , 那么我们就可以排除这个数组的这一部分

然后我们递归处理两个数组 , 直到 其中一个数组的长度为 0, 此时我们直接通过下标求出中位数即可

代码实现

注意计算 第k小数字的时候 , 使用的左右区间均为闭区间

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int m=nums1.length,n=nums2.length;
        //  +1 +2 保证left right相差1 
        int left= (m+n+1)/2;  
        int right=(m+n+2)/2;  
        return (getKth(nums1,0,m-1,nums2,0,n-1,left)+getKth(nums1,0,m-1,nums2,0,n-1,right))/2.0;
    }
    // 求两个数组中第k小的数字
    int getKth(int[] nums1, int start1, int end1, int[] nums2, int start2, int end2, int k) {
        // 由于使用的是 [ ]闭区间, 因此长度需要 +1
        int len1= end1-start1+1;
        int len2= end2-start2+1;
        // 我们调整位置, 使得计算的时候 len1 永远小于len2 => 为了方便下面的计算
        if(len1>len2) return getKth(nums2,start2,end2,nums1,start1,end1,k);
        //如果len1 ==0 , 此时只需要求 nums2 的 第k 小的数字即可
        if(len1==0)  return nums2[start2+k-1];
        //特殊情况, k=1 , 直接返回两个数组中较小的那个数字
        if(k==1) return Math.min(nums1[start1],nums2[start2]);
        trick
        // 以下是 一般情况, 的计算过程
        // 计算前几个数字的 最后的那个数字 下标 , 考虑start1=0 来推导边界值  
        int i= start1+Math.min(len1,k/2)-1;
        int j= start2+Math.min(len2,k/2)-1;
        if(nums1[i]<nums2[j]){
            // 排除数组1 的前面几个元素(k/2)
            return getKth(nums1,i+1,end1,nums2,start2,end2,k-(i-start1+1));
        }else{
            // 排除数组2 的前面几个元素(k/2)
            return getKth(nums1,start1,end1,nums2,j+1,end2,k-(j-start2+1));
        }
    }
}

20. 有效的括号

难度简单3654

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。
  3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = “()”
输出：true
示例 2：

输入：s = “()[]{}”
输出：true
示例 3：

输入：s = “(]”
输出：false

提示：

  • 1 <= s.length <= 104
  • s 仅由括号 '()[]{}' 组成

注意需要保证括号次序的合理性

我们使用一个栈来保存遍历到的括号, 如果遇到了相应的 有括号 , 那么久pop ,

比如对于(()] , 最后在栈里面保存的内容应该是( , 因为我们遍历到 ] 就可以确定当前的序列不合法了

如果当前遍历到的括号是左括号 , 那么我们直接添加

如果是右括号, 需要与 前面的那个括号对应

比如我们已经在栈里面

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean isValid(String s) {
        Stack<Character> left=new Stack<>();
        char[]chars=s.toCharArray();
        for(char c:chars){
            if(c=='(' || c=='[' || c=='{'){
                left.push(c);
            }else{
                if(left.size()!=0 && leftOf(c) == left.peek()){
                    left.pop();
                }else{
                    return false;
                }
            }
        }
        return left.size()==0;
    }
    
    char leftOf(char c){
        if(c==')') return '(' ;
        else if(c=='}') return '{';
        else return '[';
    }
}

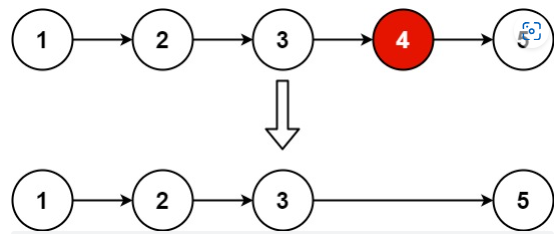
19. 删除链表的倒数第 N 个结点

难度中等2345

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]
示例 2：

输入：head = [1], n = 1
输出：[]
示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

本题使用快慢指针的做法非常简单 , 不再赘述

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    // 双指针
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode fast= head,slow=head;
        for(int i=0;i<n;i++) fast=fast.next;
        if(fast==null) return head.next; // fast为空说明需要删除的是第一个节点
        while(fast.next!=null){
            fast=fast.next;
            slow=slow.next;
        }
        // slow现在是需要删除的节点
        slow.next=slow.next.next;
        return head;
    }
}

另一种做法是 递归

需要注意的是我们是先递归, 再执行操作, 同时使用cur来统计节点的次序

  • 注意是先递归 , 再统计 , 也就是 自底向上 递归 , 那么我们统计的cur==n的时候, 说明当前的节点就是需要删除的节点
1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    int cur=0;//统计节点次序
    // 递归 , 找到倒数第n个节点并删除, 如果不是需要删除的节点那么就直接返回
    public ListNode removeNthFromEnd(ListNode head, int n) {
        if(head==null) return null;
        // 先递归
        head.next=removeNthFromEnd(head.next,n);
        cur++;
        if(cur==n) return head.next;
        return head;
    }
}

22. 括号生成

labuladong 题解思路

难度中等3006

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]
示例 2：

输入：n = 1
输出：[“()”]

提示：

  • 1 <= n <= 8

简单回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    // 回溯
    List<String> res=new ArrayList<>();
    public List<String> generateParenthesis(int n) {
        traverse(new StringBuilder(""), n,n);
        return res;
    }
    void traverse(StringBuilder sb,int left,int right){
        // 如果 左括号剩下的多, 说明生成的序列一定是不合法的 , 
        if(right<left || left<0 || right<0) return ;
        if(left==right && left == 0){
            res.add(sb.toString());
            return ;
        }
        // 尝试添加(
        sb.append("(");
        traverse(sb,left-1,right);
        sb.deleteCharAt(sb.length()-1);

        // 尝试添加)
        sb.append(")");
        traverse(sb,left,right-1);
        sb.deleteCharAt(sb.length()-1);
    }
}

23. 合并K个升序链表

难度困难2285

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2：

输入：lists = []
输出：[]
示例 3：

输入：lists = [[]]
输出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按 升序 排列
lists[i].length 的总和不超过 10^4

分治

考虑分治的思想, 将链表数组切割成 多个的两个链表 , 然后将k个链表合并的问题 简化成 合并两个有序链表

其实就是归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    // 分治
    public ListNode mergeKLists(ListNode[] lists) {
        return merge(lists,0,lists.length-1);
    }
    ListNode merge(ListNode[]lists,int i,int j){
        if(i==j) return lists[i];
        if(i>j) return null;
        int mid= i+ (j-i)/2;
        return merge2Lists(merge(lists,i,mid),merge(lists,mid+1,j));
    }
    ListNode merge2Lists(ListNode l1 ,ListNode l2){
        //合并两个 有序链表
        ListNode res=new ListNode(-1);
        ListNode cur=res;
        while(l1!=null && l2 !=null){
            if(l1.val <= l2.val){
                cur.next=new ListNode(l1.val);
                l1=l1.next;
            }else {
                cur.next=new ListNode(l2.val);
                l2=l2.next;
            }
            cur=cur.next;
        }
        if(l1!=null){
            cur.next=l1;
        }
        if(l2!=null){
            cur.next=l2;
        }
        return res.next;
    }
}

优先队列

我们首先初始化 一个小根堆 , 然后将数组 里面的链表的头结点全部添加到 优先队列中 ,

然后依次 poll() 优先队列的头结点 ,

  • 如果链表还指向下一个节点那么就继续添加这个节点

注意判断 数组 或者 链表为空的情况

[] , [[]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    // 使用优先队列
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0) return null;
        // PriorityQueue
        ListNode res=new ListNode(-1);
        ListNode cur=res;
        PriorityQueue<ListNode> pq=new PriorityQueue<>(lists.length,(a,b)-> a.val-b.val); // 初始化小根堆
        for (ListNode head : lists) {
            if(head!=null)
                pq.add(head);
        }
        while(pq.size()!=0){
            ListNode tmp=pq.poll();
            cur.next=tmp;
            if(tmp.next!=null){
                pq.add(tmp.next);
            }
            cur=cur.next;
        }
        return res.next;
    }
}

31. 下一个排列

难度中等2017

整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

  • 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

  • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
  • 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
  • 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须** 原地 **修改，只允许使用额外常数空间。

示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]
示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]
示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 100

例如 2, 6, 3, 5, 4, 1 这个排列， 我们想要找到下一个刚好比他大的排列，

可以从后往前看 , 我们先看后两位 4, 1 能否组成更大的排列，答案是不可以，同理 5, 4, 1也不可以

直到3, 5, 4, 1这个排列，因为 3 < 5， 我们可以通过重新排列这一段数字，来得到下一个排列 因为我们需要使得新的排列尽量小，

所以我们从后往前找第一个比3更==大==的数字，发现是4 然后，我们调换3和4的位置，得到4, 5, 3, 1这个数列

因为我们需要使得新生成的数列尽量小，于是我们可以对5, 3, 1进行排序，

可以发现在这个算法中，我们得到的末尾数字一定是倒序排列的，于是我们只需要把它反转即可

最终，我们得到了4, 1, 3, 5这个数列
完整的数列则是2, 6, 4, 1, 3, 5

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public void nextPermutation(int[] nums) {
        int i=nums.length-2;
        while(i>=0 && nums[i] >= nums[i+1]) i--; // 找到第一个逆序的数字
        // 此时这个数字是比较小的
        if(i<0){// 如果 都是顺序(从小到大的) , 直接返回最小的 顺序
            Arrays.sort(nums);
            return ; 
        }
        int j=i+1;
        for(int k=j+1; k<nums.length ;k++){ // 找到第一个比 当前位置元素大的数字
            // 需要注意 nums[k] ==nums[j] , 此时应该 取j=k , 因为我们需要使得 需要交换的两个位置尽量靠后 , 或者可以直接倒着 找
            if(nums[k]>nums[i] && nums[k]<=nums[j]){
                j=k;
            }
        }
        swap(nums,i,j); // 交换两个数字, 构成较大的序列
        reverse(nums,i+1,nums.length-1); //由于原本的后面的这一批数字都是从大到小 , 现在需要变成从小到大使得他们满足 下一个 排列
        //  后面的 序列是需要从小到大有序的
    }
    void swap(int[]nums,int i,int j){
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }
    void reverse(int[]nums,int i, int j){
        while(i<j){
            swap(nums,i++,j--);
        }
    }
}

简洁版写法

  • 查找第一个较大数字的 顺序 由 从左到右 改成 从右到左
  • reverse() 替换成了 Arrays.sort() , 在本题中两者起到的作用是相同的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public void nextPermutation(int[] nums) {
        int i=nums.length-2;
        while(i>=0 && nums[i] >= nums[i+1]) i--; // 找到第一个逆序的数字
        if(i<0){// 如果 都是顺序(从小到大的) , 直接返回最小的 顺序
            Arrays.sort(nums);
        }else{
            int j=nums.length-1;
            while(j>i && nums[j]<= nums[i]) j--; 
            swap(nums,i,j);
            Arrays.sort(nums,i+1,nums.length);
        }
    }
    void swap(int[]nums,int i,int j){
        int tmp=nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }
}

32. 最长有效括号

难度困难2119

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

1
2
3
输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

示例 2：

1
2
3
输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

示例 3：

1
2
输入：s = ""
输出：0

提示：

  • 0 <= s.length <= 3 * 104
  • s[i] 为 '(' 或 ')'

DP

所以，我们先看第 i 个位置，这个位置的元素 s[i]可能有如下两种情况：

  • s[i] =='('

    此时左括号不可能是合法括号子串的结尾 , 那么dp[i-1]=0

  • s[i] ==')'

    这时，需要看其前面对元素来判断是否有有效括号对。

    • s [i−1]==′(′

      即s[i]和s[i-1]组成一对有效括号，有效括号长度新增长度2，i 位置对最长有效括号长度为其之前2个位置的最长括号长度加上当前位置新增的2，

      我们无需知道i-2位置对字符是否可以组成有效括号对。
      那么有： dp[i]=dp[i-2] +2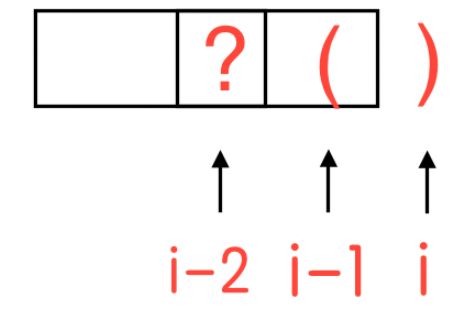

    • s [i−1]==′)′

      这种情况下，如果前面有和s[i]组成有效括号对的字符，即形如((....))，这样的话，

      就要求s[i - 1]位置必然是有效的括号对，否则s[i]无法和前面对字符组成有效括号对。

      这时，我们只需要找到和s[i]配对对位置，并判断其是否是 (即可。

      和其配对对位置为：i - dp[i - 1] - 1 。

      如果：s[i - dp[i - 1] - 1] == '('

      有效括号长度新增长度 2，i 位置对最长有效括号长度为 i-1位置的最长括号长度加上当前位置新增的 2，

      那么有： dp[i] = dp[i - 1] + 2

      值得注意的是，i−dp[i−1]−1 和 i 组成了有效括号对，这将是一段独立的有效括号序列，如果之前的子序列是形如 (…)(…) 这种序列，那么当前位置的最长有效括号长度还需要加上这一段。所以：

      dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int longestValidParentheses(String s) {
        Stack<Integer> stack = new Stack<>();
        char[]chars=s.toCharArray();
        int res=0; 
        //记录 leftIndex 相邻合法括号子串的长度，才能得出题目想要的正确结果。
        int[]dp=new int[chars.length+1]; // dp[i]表示 下标i-1 结尾的 字符串的 最长的有效括号的长度
        for(int i=0 ;i< chars.length; ++i){ //  每次 +1的条件就是添加了当前的括号之后 合法
            if(chars[i]=='('){ 
                // 遇到左括号，记录索引
                stack.push(i);
                //左括号不可能是合法括号子串的结尾
                dp[i+1]=0;
            }else{
                if(stack.size()!=0){
                    int leftIdx= stack.pop();
                    dp[i+1]= i-leftIdx+1 + dp[leftIdx];
                }else{
                    dp[i+1]=0;
                }
            }
            res=Math.max(res,dp[i+1]);
        }
        return res;
    }
}

贪心

贪心的方法与普通的统计有效括号 的方法 类似

我们使用两个变量来统计遍历过程中遇到的左右括号数量

left, right 分别统计左括号与右括号的数量

在每次的 从左到右 遍历过程中会有三种情况

  1. left<right 继续进行下一轮即可

  2. left==rigth 此时子串是有效括号 , 长度为 left *2

  3. right>left 此时 由于是从左到右遍历, 已经是非法括号了, 此时我们重置left, right

    比如())

只进行从左到右的贪心会 ==遗漏== 类似(() 的子串 , 因此我们需要反向贪心一轮

在贪心的过程中统计 最长的子串, 最后返回即可

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int longestValidParentheses(String s) {
        char[]chars=s.toCharArray();
        int res=0; 
        int left=0,right=0;
        for(int i=0 ;i< chars.length; ++i){ //  每次 +1的条件就是添加了当前的括号之后 合法
            if(chars[i]=='(') left++;
            else right++;
            if(left==right){
                res=Math.max(res,left*2);
            }else if(right > left){
                //'())' 显然已经不可能成为有效括号了
                left=0;
                right=0;
            }
        }
        left=0;
        right=0;
        // 贪心两次是因为如果 从左到右遇到了 (() 就不会计算在内 , 因此需要再反向贪心一次
        for(int i=chars.length-1;i>=0;i--){
            if(chars[i]=='(') left++;
            else right++;
            if(left==right){
                res=Math.max(res,left*2);
            }else if(left > right){
                //同理
                left=0;
                right=0;
            }
        }
        return res;
    } 
}

33. 搜索旋转排序数组

难度中等2434

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

1
2
输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

1
2
输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

1
2
输入：nums = [1], target = 0
输出：-1

提示：

  • 1 <= nums.length <= 5000
  • -104 <= nums[i] <= 104
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
  • -104 <= target <= 104

我们 根据旋转点 可以把数组分成两个区间, 然后二分

如果nums[mid] < nums[right], 那么说明此时的mid是处于旋转点的 右侧, 并且 [mid,right] 是有序的 , 反之 , [left,mid) 是有序的

知道了有序数组的区间之后 , 我们只需要进行二分即可,

==注意临界点处理==

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int search(int[] nums, int target) {
        //这个旋转数组 , 起始点必然是中间的某一个点
        // 分成左右两个区间, 左边区间的元素一定大于等于 右边的元素
        int left=0, right=nums.length-1;
        int mid= left+(right-left)/2;;
        while(left<=right){
            mid= left+(right-left)/2;
            if(nums[mid]==target){
                return mid;
            }else if(nums[mid]<nums[right]){ //此时说明右边的数组是有序的 mid 处于右边的区间
                if(nums[mid]<target && target<=nums[right]) left=mid+1;
                else right=mid-1;
            }else{ // 此时说明左边的数组是有序的mid处于左边的区间
                if(nums[left]<=target && target<nums[mid]) right=mid-1;
                else left=mid+1;
            }
        }
        return -1;
    }
}

42. 接雨水

labuladong 题解思路

难度困难4014

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

1
2
3
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

1
2
输入：height = [4,2,0,3,2,5]
输出：9

提示：

  • n == height.length
  • 1 <= n <= 2 * 104
  • 0 <= height[i] <= 105

暴力法

遍历高度 , 从当前的height[i]向左右两边展开, 统计左右两边柱子的最高高度, 取最小值 , 减去height[i]就是当前的柱子可以存储的雨水量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int trap(int[] height) {
        int res=0;
        for(int i=1;i<height.length-1 ;i++){
            int maxL=0,maxR=i+1;
            for(int j=0;j<i;j++){
                if(height[j]>=height[maxL]) maxL=j; 
            }
            for(int j=i+1;j<height.length;j++){
                if(height[j]>=height[maxR]) maxR=j; 
            }
            res+=Math.max(Math.min(height[maxR],height[maxL])-height[i],0);
        }
        return res;
    }
}

DP

前面的计算左右两边高度的过程 , 仔细观察可以发现我们实际上做了很多的重复计算 ,

比如我们需要计算height[i]的左边最高的柱子, 那么在计算的过程中这个可以简化为

Math.max(maxL[i-1],height[i-1])

我们可以把这个计算的中间过程用数组存储起来然后单独进行计算

1
2
3
for(int i=1;i<height.length ;i++){
    maxL[i]=Math.max(maxL[i-1],height[i-1]);
}

对于maxR同理

1
2
3
for(int i=height.length-2;i>=0 ;i--){
    maxR[i]=Math.max(maxR[i+1],height[i+1]);
}

然后我们最后遍历一遍柱子, 累加每个柱子可以存储的雨水量

1
2
3
for(int i=1;i<height.length-1 ;i++){
    res+=Math.max(Math.min(maxL[i],maxR[i])-height[i],0);//雨水量不会为负
}

那么总体的代码就是

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int trap(int[] height) {
        int[]maxL=new int[height.length];
        int[]maxR=new int[height.length];
        int res=0;
        maxL[0]=height[0];
        maxR[height.length-1]=height[height.length-1];
        for(int i=1;i<height.length ;i++){
            maxL[i]=Math.max(maxL[i-1],height[i-1]);
        }
        for(int i=height.length-2;i>=0 ;i--){
            maxR[i]=Math.max(maxR[i+1],height[i+1]);
        }
        for(int i=1;i<height.length-1 ;i++){
            res+=Math.max(Math.min(maxL[i],maxR[i])-height[i],0);
        }
        return res;
    }
}

可以优化为

统计最大高度的时候把当前的柱子也计算在内, 最后在遍历的时候就不用使用Math.max(rain[i],0)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
    public int trap(int[] height) {
        int[]maxL=new int[height.length];
        int[]maxR=new int[height.length];
        int res=0;
        maxL[0]=height[0];
        maxR[height.length-1]=height[height.length-1];
        for(int i=1;i<height.length ;i++){
            maxL[i]=Math.max(maxL[i-1],height[i]);
        }
        for(int i=height.length-2;i>=0 ;i--){
            maxR[i]=Math.max(maxR[i+1],height[i]);
        }
        for(int i=1;i<height.length-1 ;i++){
            res+=Math.min(maxL[i],maxR[i])-height[i];
        }
        return res;
    }
}

49. 字母异位词分组

难度中等1341

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的字母得到的一个新单词，所有源单词中的字母通常恰好只用一次。

示例 1:

1
2
输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

1
2
输入: strs = [""]
输出: [[""]]

示例 3:

1
2
输入: strs = ["a"]
输出: [["a"]]

提示：

  • 1 <= strs.length <= 104
  • 0 <= strs[i].length <= 100
  • strs[i] 仅包含小写字母

排序

字母相同，但排列不同的字符串，排序后都一定是相同的。因为每种字母的个数都是相同的，那么排序后的字符串就一定是相同的。

这里可以利用 stream 的 groupingBy 算子实现直接返回结果：

1
2
3
4
5
6
7
8
9
10
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        return new ArrayList<>(Arrays.stream(strs)
                               .collect(Collectors.groupingBy(str->{
                                   char[] chars = str.toCharArray();
                                   Arrays.sort(chars);
                                   return new String(chars);
                               })).values());
    }
}

注意 groupingBy 算子计算完以后，返回的是一个 Map<String, List<String>>，map 的键是每种排序后的字符串，值是聚合的原始字符串，我们只关心值，所以我们最后 new ArrayList<>(map.values())。

计数

使用特殊的 标记 来标记每一个异位词 , 注意需要保证不发生key冲突

把相同标记的 string放到List里面, 最后返回结果

注意不要使用单纯的加法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> map = new HashMap<>();
        for(String s:strs){
            String key=check(s);
            if(!map.containsKey(key)){
                List<String> list=new ArrayList();
                list.add(s);
                map.put(key,list);
            }else{
                map.get(key).add(s);
            }
        }
        return new ArrayList(map.values());
    }
    String check(String s){
        // 如果使用单纯的加法 , 那么会出问题 a+y=b+z
        char[]chars=s.toCharArray();
        char[]count=new char[26];
        int res=0;
        for(char c: chars){
            count[c-'a']++;
        }
        return new String(count);
    }
}

72. 编辑距离

难度困难2719

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

示例 1：

1
2
3
4
5
6
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：

1
2
3
4
5
6
7
8
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

提示：

  • 0 <= word1.length, word2.length <= 500
  • word1 和 word2 由小写英文字母组成

非常经典的动态规划问题

根据题目我们可以知道总共有三种操作, 插入/删除/替换 , 但是插入/删除操作本质上是一样的

比如A, B 两个字符串 , 分别为 'ab' , 'b' , 我们对他们两个操作 , 可以对A 删除a ,

也可以对B插入a

那么我们结合动态规划的思想 , 定义dp[i][j] 表示两个字符串分别有 i , j 个字符参与统计时候需要的==操作次数== , 那么就有

dp[i][0],dp[j][0] 对于第一行, 第一列数据, 我们只能做插入/删除操作 , 因此他们需要的操作数是 i, j个。

那么对于一般情况 dp[i][j] , 可以分成以下两种情况讨论

  • s1[i-1] == s2[j-1] , 这个时候 dp[i][j] = dp[i-1][j-1] , 因为我们对于当前的两个字符不需要做任何操作就可以使他们保持相同

  • s1[i-1] != s2[j-1] , 这个时候我们可以通过三个数据来得到dp[i][j]

    分别是通过dp[i-1][j] , dp[i][j-1] , dp[i-1][j-1]

    1. 对于dp[i-1][j] , 其实就是多了一个s2[j-1]位置的字符, 因此我们此时是

      dp[i][j]=dp[i-1][j]+1

    2. 对于dp[i][j-1]同理

    3. 对于dp[i-1][j-1] , 就相当于我们进行了交换操作 , 此时有

      dp[i][j] = dp[i-1][j-1]+1 , 对于这个交换操作 , 我们需要知道的就是此时

      dp[i-1][j-1] 小于dp[i-1][j] ,dp[i][j-1] , 那么就是对应的交换操作

    那么以上三种情况是一样的 , 直接用

    dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;

    即可

最后我们返回dp[m][n] , 表示参与统计的m ,n 个字符需要变成相同的字符串的操作次数

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int minDistance(String word1, String word2) {
        // 一共有三种操作, 插入/删除/替换
        // 那么插入删除其实本质上是一样的, 我对这个插入 ,就等价于对另一个做删除
        // dp[i][j] 表示w1 i, w2 j 结尾的字符串 转换成相同字符串需要的最少操作
        int m=word1.length(),n=word2.length();
        char[]w1=word1.toCharArray();
        char[]w2=word2.toCharArray();
        int[][]dp=new int[m+1][n+1];
        for(int i=0;i<=m;i++) dp[i][0]=i; // 需要插入/删除i个字符        
        for(int i=0;i<=n;i++) dp[0][i]=i;
        for(int i=1;i<=m;i++){
            for(int j=1;j<=n;j++){
                // 如果两个字符串相同
                if(w1[i-1]==w2[j-1]){// 注意 字符个数与下标的对应情况
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    // 需要对当前的字符 做出 相应操作 : 插入/删除/替换
                    dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1;
                }
            }
        }
        return dp[m][n];
    }
}

75. 颜色分类

难度中等1484

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，**原地**对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 1：

1
2
输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

1
2
输入：nums = [2,0,1]
输出：[0,1,2]

提示：

  • n == nums.length
  • 1 <= n <= 300
  • nums[i] 为 0、1 或 2

一个很有意思的思路 , 我们使用三个变量来统计 2 1 0的下一个该放的下标 ,

因此初始化为 0

比如下面的序列 2,0,2,1,1,0

我们首先遍历2 , 对于那么对于2 , 他的下一个下标就+1 , num2=1 , 此时的序列是 2

对于0 , 由于我们需要使得整个数组有序 , 因此当遍历到0 , 三个变量都应该+1 , 然后我们进行赋值 , 此时的序列就变成了 0 2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public void sortColors(int[] nums) {
        int num0=0,num1=0,num2=0;
        for(int num:nums){
            if(num==0){
                nums[num2++]=2;
                nums[num1++]=1;
                nums[num0++]=0;
            }else if(num==1){
                nums[num2++]=2;
                nums[num1++]=1;
            }else{
                nums[num2++]=2;
            }
        }
    }
}

知识点 🍓

PriorityQueue

PriorityQueue底层实现是 堆 , 默认采用的是小根堆

Java PriorityQueue类是一种队列数据结构实现，其中根据优先级处理对象。它与遵循FIFO（先进先出）算法的标准队列不同。

在优先级队列中，添加的对象根据其优先级。默认情况下，优先级由对象的自然顺序决定。队列构建时提供的比较器可以覆盖默认优先级。

PriorityQueue构造器

PriorityQueue类提供了6种在Java中构造优先级队列的方法。

  • PriorityQueue（）：使用默认初始容量（11）构造空队列，该容量根据其自然顺序对其元素进行排序。
  • PriorityQueue（Collection c）：构造包含指定集合中元素的空队列。
  • PriorityQueue（int initialCapacity）：构造具有指定初始容量的空队列，该容量根据其自然顺序对其元素进行排序。
  • PriorityQueue（int initialCapacity，Comparator comparator）：构造具有指定初始容量的空队列，该容量根据指定的比较器对其元素进行排序。
  • PriorityQueue（PriorityQueue c）：构造包含指定优先级队列中元素的空队列。
  • PriorityQueue（SortedSet c）：构造包含指定有序集合中元素的空队列。

PriorityQueue方法

PriorityQueue类主要有下面几个主要的方法。

  • boolean add（object）：将指定的元素插入此优先级队列。
  • boolean offer（object）：将指定的元素插入此优先级队列。
  • boolean remove（object）：从此队列中删除指定元素的单个实例（如果存在）。
  • Object poll（）：检索并删除此队列的头部，如果此队列为空，则返回null。
  • Object element（）：检索但不删除此队列的头部，如果此队列为空，则返回null。
  • Object peek（）：检索但不删除此队列的头部，如果此队列为空，则返回null。
  • void clear（）：从此优先级队列中删除所有元素。
  • Comparator comparator（）：返回用于对此队列中的元素进行排序的比较器，如果此队列根据其元素的自然顺序排序，则返回null。
  • boolean contains（Object o）：如果此队列包含指定的元素，则返回true。
  • Iterator iterator（）：返回此队列中元素的迭代器。
  • int size（）：返回此队列中的元素数。
  • Object [] toArray（）：返回包含此队列中所有元素的数组。