-
作业中编程相关题目均使用Java实现
-
关于用到的类的具体实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
|
练习1
2
树形结构, 其中a没有前驱结点, 为根节点, b e i g 没有后继节点, 为叶子结点
8
(1)
1
2
3
4
5
6
7
| public long sumArray(int[]nums){
long res=0;
for(int i=0;i<nums.length;i++){
res+=nums[i];
}
return res;
}
|
(2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| public void printNumsByASC(long a,long b,long c){
if(a>b) {
if (b > c) {
System.out.println("" + c + " " + b + " " + a);
} else {
System.out.println("" + b + " " + c + " " + a);
}
}else{
if (a > c) {
System.out.println("" + c + " " + a + " " + b);
} else {
System.out.println("" + Math.max(b,c) + " " + Math.min(b,c) + " " + a);
}
}
}
|
(3)
1
2
3
4
5
6
7
8
9
| public void printMaxAndMin(int[]nums){
if(nums.length==0) return ;
int maxNum=nums[0],minNum=nums[0];
for(int i=1;i<nums.length ;i++){
maxNum= Math.max(nums[i],maxNum);
minNum= Math.min(nums[i],minNum);
}
System.out.println("max:" + maxNum +"\nmin: "+ minNum);
}
|
9
f(n)= 100n3 + n2 + 1000= O(n3)
f(n)= 25n3 + 5000n2 = O(n3)
h(n)= n1.5 + 5000nlog2n , n->∞ 时 , √n > log2n , 故 h(n) =O(n1.5)
11
(1)假设while循环语句执行次数为T(n),
则: i=2T(n)+1≤n,
那么有 T(n)≤(n-1)/2=O(n)。
(2)算法中的基本运算语句是f(b[>b[])k=j,其执行次数T(n)为:
T(n) = n(n-1)/2 = O(n2)
(3)设while循环语句执行次数为T(n),则:
s=1+2+ … +T(n) <= n ,则 T(n)=0(√n)。
练习2
1
分别为顺序存储结构以及链式存储结构
- 链式存储结构的内存地址不一定是连续的,但顺序存储结构的内存地址一定是连续的;
- 链式存储适用于在较频繁地插入、删除、更新元素时,而顺序存储结构适用于频繁查询时使用。
- 空间上 , 顺序比链式节约空间。是因为链式结构每一个节点都有一个指针存储域。
- 存储操作上 , 顺序支持随机存取,方便操作
4
在顺序表L中找到第一个值最大的元素并删除
5
在顺序表L中找到最后一个值最小的元素并在该位置插入一个值为x的元素
12
由题意可知 , 本题其实就是反转链表 , 代码实现如下
1
2
3
4
5
6
7
8
9
10
11
12
| public ListNode reverseList(ListNode head) {
if(head==null || head.next==null) return head;
ListNode cur = head;
ListNode pre = null;
while(cur!=null){
ListNode tmp = cur.next;
cur.next=pre;
pre=cur;
cur=tmp;
}
return pre;
}
|
15
由题意可知 , 本题其实就是归并排序链表 , 不过需要注意空间复杂度 , 代码实现如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| public ListNode sortList(ListNode head) {
if(head==null || head.next==null) return head;
return split(head);
}
public ListNode split(ListNode head){
if(head.next==null) return head;
ListNode slow = head, fast= head.next;
while(fast!=null && fast.next!=null){
slow=slow.next;
fast=fast.next.next;
}
ListNode tmp = slow.next;
slow.next=null;
ListNode left= split(head);
ListNode right= split(tmp);
return mergeList(left,right);
}
public ListNode mergeList(ListNode left,ListNode right){
ListNode cur= new ListNode(-1);
ListNode res = cur;
while(left!=null && right != null){
if(left.val<=right.val){
cur.next= left;
left=left.next;
cur=cur.next;
}else{
cur.next= right;
right=right.next;
cur=cur.next;
}
}
if(left!=null){
cur.next=left;
}
if(right!=null){
cur.next=right;
}
return res.next;
}
|
练习3
1
CDBAE
CDBEA
CDEBA
2
| 方案 |
优点 |
缺点 |
| 1 |
每个栈用一个顺序存储空间时,操作简单 |
各栈不能共享空间 , 不容易进行空间的合理分配。 |
| 2 |
相比方案一充分地利用了空间, 不容易产生溢出 |
在查询,移动元素的时候十分消耗时间 |
| 3 |
不需要考虑栈的溢出的问题 |
由于栈中的元素需要使用指针连接, 因此会比较耗费空间 |
5
算法的功能是删除栈中值为x 的元素
6
算法的功能是删除队列中第i个元素
12
使用一个临时栈来存储元素来完成队列的反转
1
2
3
4
5
6
7
8
9
| public void reverseQueue(LinkedList<Integer> que){
Stack<Integer> tmp = new Stack<>();
while(que.size()!=0){
tmp.push(que.poll());
}
while(tmp.size()!=0){
que.add(tmp.pop());
}
}
|
练习6
2
(1) 元素 a1,6,8 的起始位置为 1000+ 2*( 1*9*10 + 6*10 + 8 ) = 1316
(2) 数组a所占的存储空间为 1440 Bytes
6
采用三元组存储。
我们可以假设稀疏矩阵 A 有 t 个非零元素,加上行数 、列数 和非零元素个数 ,那么三元组顺序表的存储空间总数为 3(t+1),
若用二维数组存储时占用存储空间总数为 m×n,只有当 3(t+1)<m×n 即 t<m×n/3-1 时才最节省空间
8
- head[(x,y,z)]=x。
- tail[((a,b),(x,y))]=((x,y))。
练习7
1
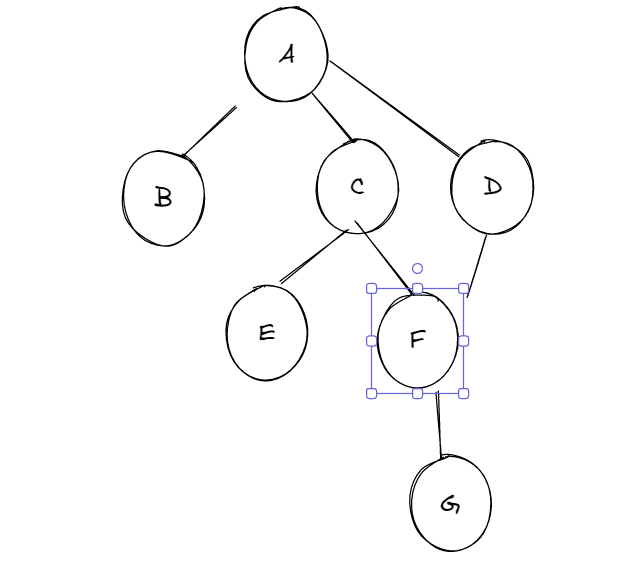
- 根结点为 A
- 叶子结点为 B、E、G、D
- 结点 C 的度为 2
- 这棵树的度为 3
- 这棵树的高度为 4
- 结点 C 的孩子结点为 E、F
- 结点 C 的双亲结点为 A
3
-
求X和Y结点的最近祖先结点
双亲存储结构
-
求X结点的所有子孙
孩子链存储结构
-
求根结点到X结点的路径
孩子兄弟存储结构
-
求X结点的所有右边结点的路径
孩子存储结构
-
判断X结点是否是叶子结点
孩子链存储结构
-
求X结点的所有孩子
孩子链存储结构
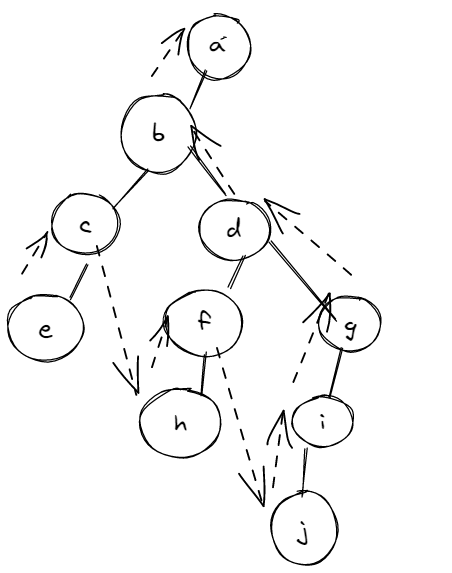
4
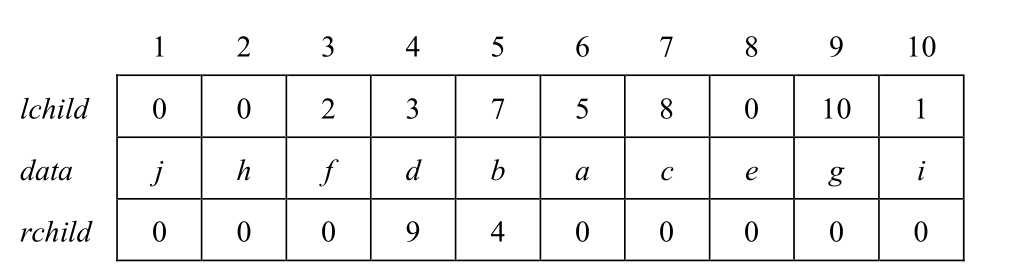
(1)
树结构如下
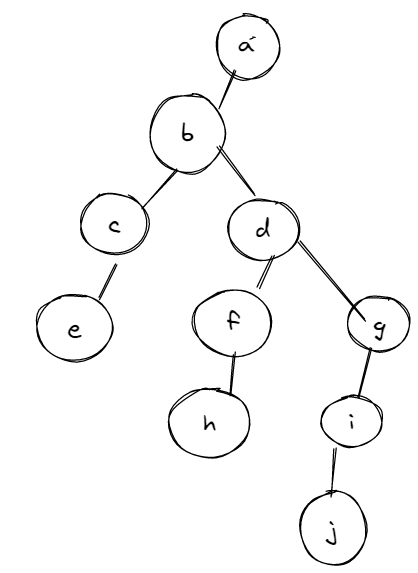
(2)
先序遍历序列为:abcedfhgij
中序遍历序列为:ecbhfdjiga
后序遍历序列为:echfjigdba
(3)
后序遍历序列为echfjigdba
6
首先我们知道完全二叉树满足叶子结点只会在最大的两层出现, 那么节点最多的情况就是第六层为倒数第二层 , 对于满二叉树第六层的节点个数为25 =32 , 而本题中要求第六层还有8个叶子结点 , 那么可得有24个非叶子节点 , 这个时候满足二叉树的节点数量最多, 为 24*2 + 26 -1 = 111
那么最少的节点个数对应的情况就是 第六层只有八个叶子结点 , 此时的二叉树的节点的个数为 8+ 25 -1= 39
第一种情况 二叉树有七层, 第二种情况二叉树有 六层
8
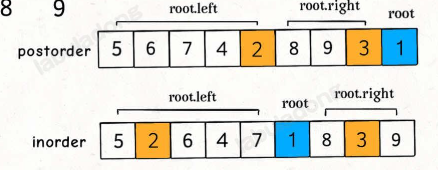
我们通过后序遍历的序列下手, 首先构建根节点的映射关系, 然后通过映射关系获取当前根节点在inorder中的index, 然后划分为左右子树 , 递归执行, 最终构建整个二叉树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
Map<Integer,Integer> map =new HashMap();
int postIdx;
public TreeNode buildTree(int[] inorder, int[] postorder) {
postIdx=postorder.length-1;
for(int i=0;i<inorder.length;i++){
map.put(inorder[i],i);
}
return build(postorder,0,inorder.length-1);
}
TreeNode build(int[]postorder,int left,int right){
if(left>right){
return null;
}
TreeNode root= new TreeNode(postorder[postIdx--]);
int mid = map.get(root.val);
root.right= build(postorder,mid+1,right);
root.left= build(postorder,left,mid-1);
return root;
}
}
|
12
统计二叉树中单分支节点的个数
1
2
3
4
5
6
7
8
9
| int cnt=0;
void dfs(TreeNode root){
if(root==null || (root.left==null && root.right==null)) return ;
if(root.left==null|| root.right==null){
cnt++;
}
dfs(root.left);
dfs(root.right);
}
|
20
注意完全二叉树的定义:
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。
BFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| boolean isCBT(TreeNode root){
if(root==null) return true;
LinkedList<TreeNode> que= new LinkedList<>();
int depth=depth(root);
int curDepth=1;
que.add(root);
while(que.size()!=0){
int size = que.size;
for(int i=0;i<size;i++){
TreeNode tmpNode = que.poll();
if(tmpNode.left==null&& tmpNode.right==null && depth-curDepth >2){
return false;
}
if(tmpNode.left!= null ) que.add(tmpNode.left);
if(tmpNode.right!= null ) que.add(tmpNode.right);
}
curDepth++;
}
return true;
}
int depth(TreeNode root){
if(root==null) return 0;
return Math.max(depth(root.left),depth(root.right)) +1;
}
|
练习8
2
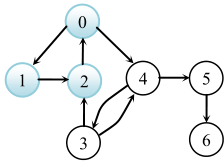
0、1、2构成一个环,这个环一定是某一个强连通分量的一部分。
那么对于顶点3、4,它们到这个环中的顶点都有双向路径,所以将3、4加入。
对于5、6,它们各自构成一个强连通分量。
因此该有向图的强连通分量有3个
4
对于邻接矩阵表示的无向图 , 边数等于邻接矩阵数组中为1的元素个数除以2;
对于邻接表表示的无向图,边数等于边结点的个数除以2。
对于邻接矩阵表示的有向图,边数等于邻接矩阵数组中为1的元素个数;
对于邻接表表示的有向图,边数等于边结点的个数
5
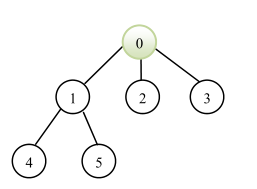
DFS
0 1 4 5 2 3
0 1 4 5 3 2
0 1 5 4 2 3
0 1 5 4 3 2
0 2 1 4 5 3
0 2 1 5 4 3
0 2 3 1 4 5
0 2 3 1 5 4
0 3 1 4 5 2
0 3 1 5 4 2
0 3 2 1 4 5
0 3 2 1 5 4
BFS
0 1 2 3 4 5
0 1 2 3 5 4
0 1 3 2 4 5
0 1 3 2 5 4
0 2 1 3 4 5
0 2 1 3 5 4
0 2 3 1 4 5
0 2 3 1 5 4
0 3 1 2 4 5
0 3 1 2 5 4
0 3 2 1 4 5
0 3 2 1 5 4
练习9
1
(1)
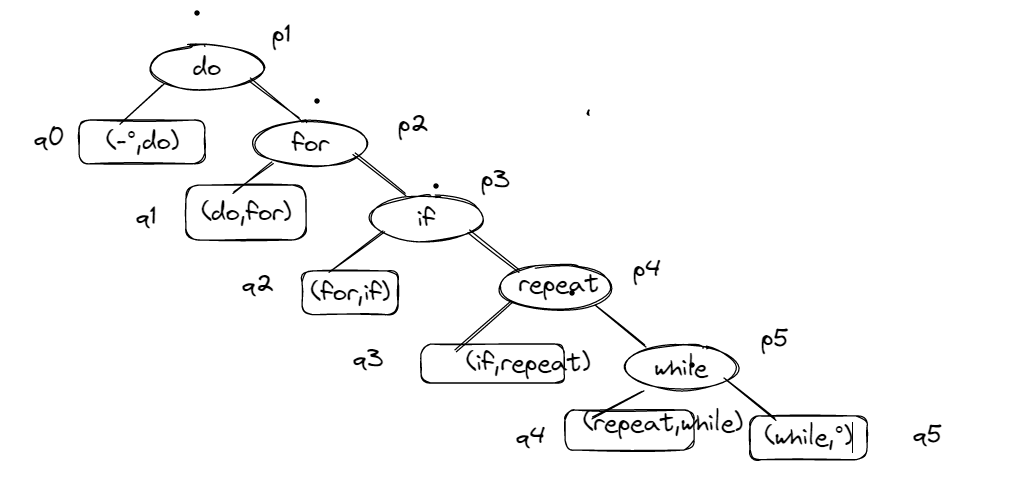
(2)
ASL成功=(1p1+2p2+3p3+4p4+5p5)=0.97
ASL不成功=(1q0+2q1+3q2+4q3+5q4+5q5)=1.07
4
(1)
二叉排序树
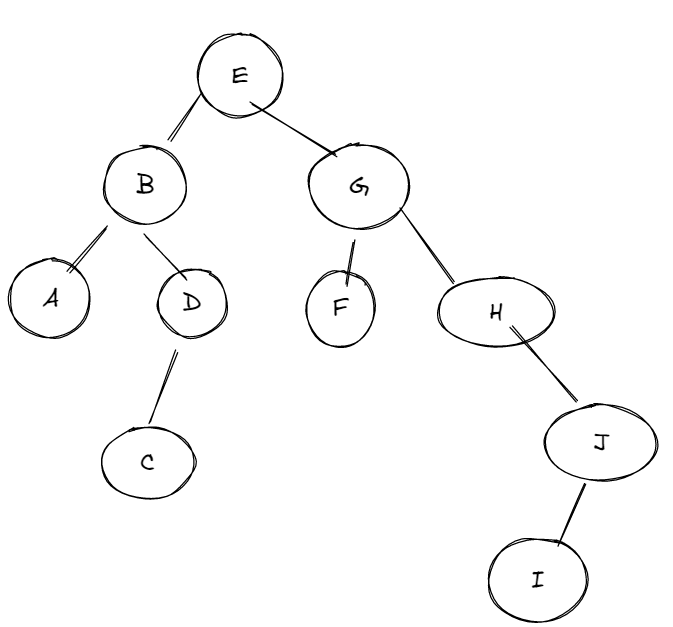
(2)
ASL成功=(1*1+2*2+4*3+2*4+1*5)/10=3
(3)
ASL不成功=(6 * 3+3*4+2 *5)/11=3.64
10
h(key)=key % 13
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public static void main(String[] args) {
HashMap<Integer, List<Integer>> map = new HashMap<>();
Scanner sc = new Scanner(System.in);
System.out.println("input the num counts");
int len= sc.nextInt();
System.out.println("input the nums");
for (int i = 0; i < len; i++) {
int num = sc.nextInt();
int key = num % 13;
List<Integer> list = map.get(key)==null?new ArrayList<Integer>():map.get(key);
list.add(num);
map.put(key,list);
}
Set<Map.Entry<Integer, List<Integer>>> entries = map.entrySet();
entries.forEach(item->{
if(item.getValue().size()>1){
System.out.println("下标为 "+ item.getKey() +" 冲突, 元素为: "+ item.getValue() + " 冲突的次数为 : "+ item.getValue().size());
}
});
}
|
构建哈希表如下
| index |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
| key |
|
1 |
14 |
55 |
27 |
68 |
19 |
20 |
84 |
|
23 |
11 |
10 |
77 |
|
|
|
|
|
| 次数 |
|
1 |
2 |
1 |
4 |
3 |
1 |
1 |
3 |
|
1 |
1 |
3 |
2 |
|
|
|
|
|
练习10
插入排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| public class InsertSort {
public static void sort(int[]nums){
for (int i = 1; i < nums.length; i++) {
int temp = nums[i];
int j =i-1;
while(j>=0&& temp < nums[j]){
nums[j+1]=nums[j];
j--;
}
nums[j+1]=temp;
System.out.println(Arrays.toString(nums));
}
}
public static void main(String[] args) {
int[] nums = Util.generateArray(10);
Util.printArray(nums);
sort(nums);
Util.printArray(nums);
}
}
|
希尔排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class ShellSort {
public static void sort(int[]nums){
int length = nums.length;
int temp;
for (int step = length / 2; step >= 1; step /= 2) {
for (int i = step; i < length; i++) {
temp = nums[i];
int j = i - step;
while (j >= 0 && nums[j] > temp) {
nums[j + step] = nums[j];
j -= step;
}
nums[j + step] = temp;
}
}
}
public static void main(String[] args) {
int[] nums = Util.generateArray(10);
Util.printArray(nums);
sort(nums);
Util.printArray(nums);
}
}
|
快速排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| public class QuickSort {
public static void sort(int[]nums,int i, int j) {
if(i>j){
return ;
}
int pivot= nums[i];
int l=i,r=j;
while(l<r){
while(l<r&&nums[r]>=pivot){
r--;
}
while(l<r&&nums[l]<=pivot){
l++;
}
if(l<r){
Util.swap(nums,l,r);
}
}
nums[i]=nums[l];
nums[l]=pivot;
sort(nums,i,l-1);
sort(nums,l+1,r);
}
public static void main(String[] args) {
int[] nums = Util.generateArray(10);
Util.printArray(nums);
sort(nums,0,nums.length-1);
Util.printArray(nums);
}
}
|
堆排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
|
public class HeapSort {
public static void main(String[] args) {
int[] nums = Util.generateArray(10);
Util.printArray(nums);
MyMaxHeap.sort(nums);
Util.printArray(nums);
}
static class MyMaxHeap{
static int heapSize=0;
static int limit = 100;
static int[] heap=new int[limit];
public void push(int val){
if(heapSize==limit){
throw new RuntimeException("heap is Full");
}
heap[heapSize]=val;
heapInsert(heap,heapSize++);
}
public static int pop(int val){
int res=heap[0];
Util.swap(heap,0,--heapSize);
heapify(heap,0,heapSize);
return res;
}
public static void heapInsert(int[]heap,int index){
while(heap[index]>heap[(index-1)/2]){
Util.swap(heap,index,(index-1)/2);
}
}
public static void sort(int[] nums){
if(nums==null||nums.length<2){
return ;
}
for (int i = nums.length-1; i >=0; i--) {
heapify(nums,i,nums.length);
}
int heapSize= nums.length;
Util.swap(nums,0,--heapSize);
while(heapSize!=0){
heapify(nums,0,heapSize);
Util.swap(nums,0,--heapSize);
}
}
public static void heapify(int[]nums,int index,int heapSize){
int left= 2*index+1;
while(left<heapSize){
int largest= left+1<heapSize&& nums[left+1]>nums[left]?left+1:left;
largest= nums[largest]>nums[index]?largest:index;
if(largest==index){
break;
}
Util.swap(nums,index,largest);
index=largest;
left= 2*index+1;
}
}
}
}
|
归并排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
| public class MergeSort {
public static void main(String[] args) {
int[] nums = Util.generateArray(10);
Util.printArray(nums);
int[] sort = sort(nums);
Util.printArray(sort);
}
public static int[] sort(int[]nums) {
int[] arr = Arrays.copyOf(nums, nums.length);
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
return merge(sort(left), sort(right));
}
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
}
|