写lc的时候写到了这个 912. 排序数组 - 力扣（LeetCode） , 我点进去一看

给你一个整数数组 nums，请你将该数组升序排列。

很快啊 , 我啪的一下就是一个快排

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] sortArray(int[] nums) {
        qs(nums,0,nums.length-1);
        return nums;
    }
    void qs(int[]nums,int i,int j){
        if(i>j) return ;
        int l=i,r=j;
        int pivot=nums[i];
        while(l<r){
            while(l<r && nums[r]>=pivot) r--;
            while(l<r && nums[l]<=pivot) l++;
            if(l<r){
                int tmp = nums[l];
                nums[l]=nums[r];
                nums[r]=tmp;
            }
        }
        nums[i]=nums[l]; 
        nums[l]=pivot; 
        qs(nums,i,l-1);
        qs(nums,l+1,j);
    }
}

结果反手收到一个TLE , , , ,

题目有一个样例是 五万个2 的数组 , , , ,

那么对于上面的这个样例，实际在执行上面的代码的时候对于每一个基准数字的复杂度都是O(N) ,也就是快排的最差的情况，此时的快速排序也就退化成了冒泡排序，

算法的运行时间的递归式可表达为：T(n) = T(0) + T(n - 1) + O(n) = T(n - 1) + O(n)，T(n)的解是O(N2)。

那么对于我们想的最理想的快排的情况，应该是每次切分之后两个数组的大小n / 2时，

这时一个的数组的大小为[n / 2 - 1]，另一个为[n / 2]，此时算法运行时间的递归式为：T(n) = 2T(n / 2) + O(n)，T(n)的解是O(nlgn)。

以下部分的代码全部都是可以直接运行的

  • JDK 1.8
  • IDEA 2022.2.3

首先我们知道快速排序使用分治的思想，通过一趟排序将待排序列分割成两部分，其中一部分记录的关键字均比另一部分记录的关键字小。之后分别对这两部分记录继续进行排序，递归地以达到整个序列有序的目的。

那么对于分治算法 , 如果每次的划分都能划分成两个等长的子序列, 那么算法的效率会最高 , 因此基准的选择十分重要

关于选择及基准的方式 , 主要有三种

  1. 固定位置 : 我们每次都取序列的第一个或者最后一个位置去作为pivot (也就是上面的写法)
  2. **随机选取基准 ** : 对于需要排序的序列是部分有序的, 如果我们固定的去选择基准, 那么效率就会比较低下, 这个时候就引入了 随机选取枢轴
  3. 三数取中 : 上面的随机选取基准的方法在最坏的情况下实际上还是 O(N2) 的时间复杂度 , 这个时候就引入了三数取中选取枢轴

准备工作

测试类

这里统一把排序的方法命名为quickSort , 然后利用反射进行测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public class QuickSortTest {
    
    /**
    * 主要测试类
    */
    static void sortTest(int[] nums, Object sort) {
        Long start = System.nanoTime();
        Class<?> clazz = sort.getClass();
        try {
            Method quickSort = clazz.getDeclaredMethod("quickSort", int[].class, int.class, int.class);
            quickSort.setAccessible(true);
            quickSort.invoke(sort,nums,0,nums.length-1);
        }catch (Exception e){
            System.out.println(e.getMessage());
        }
        System.out.println("执行耗时 : "+ (System.nanoTime()-start) + "ns");
    }

    /**
    * 打印数组
    */
    static void printNums(int[]nums){
        Arrays.stream(nums).forEach(item->{
            System.out.print(item+" ");
        });
        System.out.println();
    }

    /**
     * @param start 数字开始的范围
     * @param end 数字结束的范围
     * @param size 数组的规模
     * @return
     */
    private static int[] generateArray(int start,int end,int size){
        if(start> end || size <=0) return null;
        int[] nums = new int[size];
        for (int i = 0; i < size; i++) {
            nums[i]=start+ (int)(Math.random()*1000000%end);
        }
        return nums;
    }

    /**
    * 生成有序数组
    * @param size 数组的规模
    */
    private static int[] generateSortedArray(int size){
        int[]res=new int[size];
        int offset= (int)(Math.random()*1000); // 随机偏移量
        for (int i = 0 ; i <offset; i++) {
            res[i]=i+ offset;
        }
        return res;
    }
}

接着我们提前准备好没有任何优化的快排 , 用于对照

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public class Demo1 {
    public void quickSort(int[]nums,int i,int j){
        if(i>j) return ;
        int l=i,r=j;
        int pivot=nums[i];
        while(l<r){
            while(l<r && nums[r]>=pivot) r--;
            while(l<r && nums[l]<=pivot) l++;
            if(l<r){
                int tmp = nums[l];
                nums[l]=nums[r];
                nums[r]=tmp;
            }
        }
        nums[i]=nums[l]; 
        nums[l]=pivot; 
        quickSort(nums,i,l-1);
        quickSort(nums,l+1,j);
    }
}

随机基准法

在需要排序的序列中随机找一个数，并赋给pivot，避免固定位置法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class Demo2 {
    public void quickSort(int[]nums, int i, int j){
        Random random = new Random();
        if(i>j) return ;
        int l=i,r=j;
        // 为了避免重复元素的时候排序过慢, 需要使用随机的 pivot
        int idx = i+random.nextInt(j-i+1);
        swap(nums,idx,i);
        int pivot=nums[i];
        while(l<r){
            while(l<r && nums[r]>=pivot) r--;
            while(l<r && nums[l]<=pivot) l++;
            if(l<r){
                swap(nums,l,r);
            }
        }
        nums[i]=nums[l]; // 将left位置的数字变为基准数
        nums[l]=pivot; // 基准数字归位
        quickSort(nums,i,l-1);
        quickSort(nums,l+1,j);
    }
    void swap(int[]nums,int i,int j){
        int tmp = nums[i];
        nums[i]=nums[j];
        nums[j]=tmp;
    }
}

测试方法

已排序数组测试

1
2
3
4
5
6
7
8
9
10
11
public static void main(String[] args) {
    int start = 1234;
    int end = 1234567;
    for (int i = 0; i < 3; i++) {
        int size = (int) Math.pow(10,i+2);
        int[] nums = generateSortedArray(size);
        System.out.println("===============本轮测试数组规模 : "+ size);
        sortTest(nums,new Demo1());
        sortTest(nums,new Demo2());
    }
}

控制台输出:

可以看到前面数据少的时候差距不是很大 , 在10000个元素的时候的时间消耗已经不是一个量级了

1
2
3
4
5
6
7
8
9
10
11
12
===============本轮测试数组规模 : 100
class com.dhx.qs.Demo1执行耗时 : 392000ns
class com.dhx.qs.Demo2执行耗时 : 235900ns
===============本轮测试数组规模 : 1000
class com.dhx.qs.Demo1执行耗时 : 1487900ns
class com.dhx.qs.Demo2执行耗时 : 1369200ns
===============本轮测试数组规模 : 10000
class com.dhx.qs.Demo1执行耗时 : 17397200ns
class com.dhx.qs.Demo2执行耗时 : 1787300ns

进程已结束,退出代码0

随机数组

这里测试了几次 ,

1
2
3
4
5
6
7
8
9
10
11
12
===============本轮测试数组规模 : 100
class com.dhx.qs.Demo1执行耗时 : 134100ns
class com.dhx.qs.Demo2执行耗时 : 206000ns
===============本轮测试数组规模 : 1000
class com.dhx.qs.Demo1执行耗时 : 404100ns
class com.dhx.qs.Demo2执行耗时 : 1301400ns
===============本轮测试数组规模 : 10000
class com.dhx.qs.Demo1执行耗时 : 845700ns
class com.dhx.qs.Demo2执行耗时 : 1709600ns
===============本轮测试数组规模 : 100000
class com.dhx.qs.Demo1执行耗时 : 8881800ns
class com.dhx.qs.Demo2执行耗时 : 14566600ns

排序前检查

对于一些题目, 测试用例可能会给我们 “挖坑” , 比如直接给你一个排序好的数组 , 这个时候如果我们采用快排这种排序算法, 可能会导致时间消耗非常高 , 并且非常消耗资源 ,

同时在我们的应用中, 也可能会出现这种情况 ,

我们可以通过在排序之前对数组进行检查 ( 遍历数组 , 时间复杂度为O(N)) , 如果发现数组已经是有序的 , 那么就不需要排序了 , 直接return 即可

下面给出测试代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
public class Demo3 {
    public void quickSort(int[]nums,int i,int j){
        if(i>j) return ;
        // 加入有序性检测
        boolean isSorted = true;
        for (int k = i +1; k < j; k++) {
            if(nums[k] > nums[k-1]){
                isSorted=false;
                break;
            }
        }
        if(isSorted) return ; // 如果数组已经是有序的 , 直接return
        int l=i,r=j;
        int pivot=nums[i];
        while(l<r){
            while(l<r && nums[r]>=pivot) r--;
            while(l<r && nums[l]<=pivot) l++;
            if(l<r){
                int tmp = nums[l];
                nums[l]=nums[r];
                nums[r]=tmp;
            }
        }
        nums[i]=nums[l]; // 将left位置的数字变为基准数
        nums[l]=pivot; // 基准数字归位
        quickSort(nums,i,l-1);
        quickSort(nums,l+1,j);
    }
}

这里我们为了凸显检查的优点 , 先使用已经排序好的数组进行测试

1
2
3
4
5
6
7
8
9
10
11
public static void main(String[] args) {
    int start = 1234;
    int end = 1234567;
    for (int i = 0; i < 3; i++) {
        int size = (int) Math.pow(10,i+2);
        int[] nums = generateSortedArray(size);
        System.out.println("===============本轮测试数组规模 : "+ size);
        sortTest(nums,new Demo1());
        sortTest(nums,new Demo3());
    }
}

控制台结果打印如下 :

1
2
3
4
5
6
7
8
9
10
===============本轮测试数组规模 : 100
class com.dhx.qs.Demo1执行耗时 : 224700ns
class com.dhx.qs.Demo3执行耗时 : 204800ns
===============本轮测试数组规模 : 1000
class com.dhx.qs.Demo1执行耗时 : 1972400ns
class com.dhx.qs.Demo3执行耗时 : 953900ns
===============本轮测试数组规模 : 10000
class com.dhx.qs.Demo1执行耗时 : 18317500ns
class com.dhx.qs.Demo3执行耗时 : 19662100ns
进程已结束,退出代码0

接着我们使用没有排序的数组进行测试

1
2
3
4
5
6
7
8
9
===============本轮测试数组规模 : 100
class com.dhx.qs.Demo1执行耗时 : 309600ns
class com.dhx.qs.Demo3执行耗时 : 145200ns
===============本轮测试数组规模 : 1000
class com.dhx.qs.Demo1执行耗时 : 363500ns
class com.dhx.qs.Demo3执行耗时 : 1936800ns
===============本轮测试数组规模 : 10000
class com.dhx.qs.Demo1执行耗时 : 864000ns
class com.dhx.qs.Demo3执行耗时 : 21666500ns

通过上述结果不难得出根据适当的场景进行排序前的有序性检查还是十分有必要的, 不过如果场景不合适也可能会影响算法的性能

三取样切分

我们可以简单地来理解, 快排与归并是互补的, 归并排序将数组分成两个子数组分别排序, 并将有序的子数组归并来排序整个数组 ; 而快速排序的方式则是当两个子数组都有序时整个数组也就有序了

对于归并, 递归调用发生在处理整个数组之前

对于快排, 递归调用发生在处理整个数组之后

可以简单的把快排的过程简化如下 :

1
2
3
4
5
6
7
8
9
10
11
class Qsort{
    public static void sort(int[]nums){
        sort(nums,0,nums.length-1);
    }
    private static void sort(int[]nums,int lo,int hi){
        if(lo>hi) return ;
        int j = partition(nums,lo,hi);
        sort(a,lo,j-1);
        sort(a,j-1,hi);
    }
}

快排递归的将num[lo…hi]排序, 先用partition()方法将nums[k]放到一个合适的位置 , 然后递归的调用将其他位置的元素排序

对于快排的算法改进, 除了上面的两个方面, 还有就是切换到插入排序, 比如我们参考java中 Arrays.sort的源码 , 可以发现sort方法内部根据数组的规模来选定不同的排序算法

If the length of an array to be sorted is less than this constant, insertion sort is used in preference to Quicksort.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/**
 * If the length of an array to be sorted is less than this
 * constant, insertion sort is used in preference to Quicksort.
 */
private static final int INSERTION_SORT_THRESHOLD = 47;
/**
 * If the length of a byte array to be sorted is greater than this
 * constant, counting sort is used in preference to insertion sort.
 */
private static final int COUNTING_SORT_THRESHOLD_FOR_BYTE = 29;

/**
 * If the length of a short or char array to be sorted is greater
 * than this constant, counting sort is used in preference to Quicksort.
 */
private static final int COUNTING_SORT_THRESHOLD_FOR_SHORT_OR_CHAR = 3200;

当然类似的常量还有很多, 在此不再展开说明 , 感兴趣的可以去参考DualPivotQuicksort类

那么另外的就是接下来要说的三取样切分

三取样切分的核心思路是使用子数组的一小部分元素的中位数来切分数组 , 这样可以使得切分的效果更好, 但是代价就是需要 计算中位数

“人们发现将取样大小设为3并用大小居中的元素切分的效果更好”

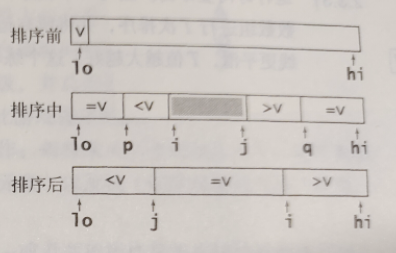
我们简单的把数组切割成这样的三个部分, 分别对应小于, 等于 和大于切分元素的数组元素 ,

通过维持三个指针来控制[left, lt )小于主元(pivot)，[lt, i)等于主元，[i, gt]未知，(gt, right]大于主元。

一开始，lt指向主元的位置left，gt指向right，而i从left右边接下来的第一个索引开始遍历，
每当遇到一个数，就判断它与主元之间的大小关系，有三种情况：

  • 小于主元就把这个数与lt指向的数交换，然后lt,i都自增1，然后继续遍历
  • 大于主元就把这个数与gt指向的数交换，gt自减1，此时i还得不能自增，因为它不知道gt用一个什么样的元素跟它交换，所以留到下一次循环判断交换过来的这个元素的去留
  • 等于主元就不需要进行交换，直接自增 1 就可以

代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public class Demo4 {
    private void quickSort(int[] a, int left, int right){
        if (right - left < 15) {
            insertSort(a, left, right);
            return;
        }
        swap(a, getMedian(a, left, (left + right) / 2, right), left);
        int v = a[left];
        int lt = left, i = left + 1, gt = right;

        while (i <= gt){
            int cmp = a[i]-v;
            if(a[i] < v)
                swap(a, lt++, i++);
            else if (a[i] > v)
                swap(a, i, gt--);
            else
                i++;
        }
        quickSort(a, left, lt - 1);
        quickSort(a, gt + 1, right);
    }

    private int getMedian(int[] a, int i, int j, int k){
        return a[i] > a[j]
                ? (a[i] < a[k] ? i : (a[j] > a[k] ? j : k))
                : (a[i] > a[k] ? i : (a[j] < a[k] ? j : k));
    }

    private void swap(int[] a, int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    //插入排序
    private void insertSort(int[] a, int left, int right) {
        for (int i = left; i <= right; ++i) {
            int j;
            int value = a[i];
            for (j = i - 1; j >= left && value < a[j] ; --j)
                a[j + 1] = a[j];
            a[j + 1] = value;
        }
    }
}

上面的三向切分并不完美，

虽然它解决了大量重复元素的不必要排序，将排序时间从线性对数级别降到线性级别，但它在数组元素重复不多的情况下，它的交换次数比标准的二分法多很多。

1
2
3
4
5
6
===============本轮测试数组规模 : 100
执行耗时 : 315700ns
===============本轮测试数组规模 : 1000
执行耗时 : 667800ns
===============本轮测试数组规模 : 10000
执行耗时 : 1712600ns

不过在90年代J.Bently和D.Mcllroy找到一个聪明的办法解决了这个问题。

快速三向切分用将重复元素放置于子数组两端的方式实现一个信息量最优的排序算法。

使用两个索引 p 和 q , 使得 a[1o…p-1] 和 a[q+1…hi] 的元素都和 a[1o] 相等。

使用另外两个索引 i 和 j , 使得 a[p…i-1] 小于 a[1o] , a[j+i…q]大于 a[lo]。

在内循环中加入代码，在a[i] 和 v 相当时将其与 a[p] 交换（并将p加1），在a[j]和v相等且a[i]和a[j]尚未和v进行比较之前将其与 a[q] 交换。

切分示意图

Java代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
public class Demo5 {

    private void quickSort(int[] a, int left, int right){
        if (right - left < 15) {
            insertSort(a, left, right);
            return;
        }
        swap(a, getMedian(a, left, (left + right) / 2, right), left);
        int v = a[left];
        int p = left + 1, i = p, j = right, q = j;

        while (true){
            while (i <= j){
                if (a[i] == v){
                    swap(a, i++, p++);
                }else if (a[i] < v){
                    i++;
                }else{
                    break;
                }
            }
            while (i <= j){
                if (a[i] == v){
                    swap(a, j--, q--);
                }else if (a[i] > v){
                    j--;
                }else{
                    break;
                }
            }
            if (i < j){
                swap(a, i++, j--);
            }else{
                break;
            }
        }

        if (p - left > i - p){
            adjust(a, p, i - 1, left);
        }else{
            adjust(a, left, p - 1, left + i - p);
        }

        if (right - q > q - j){
            adjust(a, j + 1, q, right - q + j);
        }else{
            adjust(a, q + 1, right, j + 1);
        }
        quickSort(a, left, left + i - p - 1);
        quickSort(a, right + j - q - 1, right);
    }

    private int getMedian(int[] a, int i, int j, int k){
        return a[i] > a[j]
            ? (a[i] < a[k] ? i : (a[j] > a[k] ? j : k))
            : (a[i] > a[k] ? i : (a[j] < a[k] ? j : k));
    }

    private void swap(int[] a, int i, int j){
        int t = a[i];
        a[i] = a[j];
        a[j] = t;
    }

    //插入排序
    private void insertSort(int[] a, int left, int right) {
        for (int i = left; i <= right; ++i) {
            int j;
            int value = a[i];
            for (j = i - 1; j >= left && value < a[j] ; --j)
                a[j + 1] = a[j];
            a[j + 1] = value;
        }
    }

    //调整数组
    private void adjust(int[] a, int start, int end, int toStart){
        for (int i = start; i <= end; ++i)
            swap(a, i, toStart++);
    }
}

剑指 Offer 40. 最小的k个数

难度简单543

输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：

1
2
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：

1
2
输入：arr = [0,1,2,1], k = 1
输出：[0]

这题的思路就是利用上面的切分的做法 , 对于完整的排序的数组 , 我们需要对全部的数组进行排序 ,

而对于本题我们直接通过快排切分排好第 K 小的数（下标为 K-1），那么它左边的数就是比它小的另外 K-1 个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // 最后一个参数表示我们要找的是下标为k-1的数
        return quickSearch(arr, 0, arr.length - 1, k - 1);
    }

    private int[] quickSearch(int[] nums, int lo, int hi, int k) {
        // 每快排切分1次，找到排序后下标为j的元素，如果j恰好等于k就返回j以及j左边所有的数；
        int j = partition(nums, lo, hi);
        if (j == k) {
            return Arrays.copyOf(nums, j + 1);
        }
        // 否则根据下标j与k的大小关系来决定继续切分左段还是右段。
        return j > k? quickSearch(nums, lo, j - 1, k): quickSearch(nums, j + 1, hi, k);
    }

    // 快排切分，返回下标j，使得比nums[j]小的数都在j的左边，比nums[j]大的数都在j的右边。
    private int partition(int[] nums, int lo, int hi) {
        int v = nums[lo];
        int i = lo, j = hi + 1;
        while (true) {
            while (++i <= hi && nums[i] < v);
            while (--j >= lo && nums[j] > v);
            if (i >= j) {
                break;
            }
            int t = nums[j];
            nums[j] = nums[i];
            nums[i] = t;
        }
        nums[lo] = nums[j];
        nums[j] = v;
        return j;
    }
}

参考